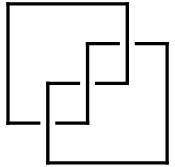
Arc Presentations
An Arc Presentation [math]\displaystyle{ A }[/math] of a knot [math]\displaystyle{ K }[/math] (in "grid form", to be precise) is a planar (toroidal, to be precise) picture of the knot in which all arcs are either horizontal or vertical, in which the vertical arcs are alway "above" the horizontal arcs, and in which no two horizontal arcs have the same [math]\displaystyle{ y }[/math]-coordinate and no two vertical arcs have the same [math]\displaystyle{ x }[/math]-coordinate (read more at [1]). Without loss of generality, the [math]\displaystyle{ x }[/math]-coordinates of the vertical arcs in [math]\displaystyle{ A }[/math] are the integers [math]\displaystyle{ 1 }[/math] through [math]\displaystyle{ n }[/math] for some [math]\displaystyle{ n }[/math], and the [math]\displaystyle{ y }[/math]-coordinates of the horizontal arcs in [math]\displaystyle{ A }[/math] are (also!) the integers [math]\displaystyle{ 1 }[/math] through [math]\displaystyle{ n }[/math].
Thus for example, on the left is an arc presentation of the trefoil knot. It can be represented numerically
KnotTheory` knows about arc presentations:
(For In[1] see Setup)
| ||||
In[2]:=
|
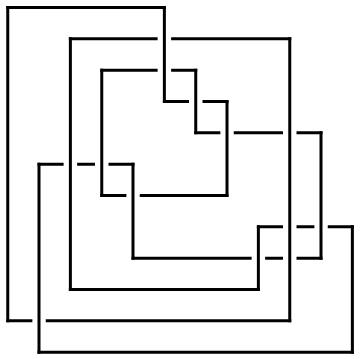
ap = ArcPresentation["K11n11"]
|
Out[2]=
|
ArcPresentation[{12, 2}, {1, 10}, {3, 9}, {5, 11}, {9, 12}, {4, 8},
{2, 5}, {11, 7}, {8, 6}, {7, 4}, {10, 3}, {6, 1}]
|
In[4]:=
|
Draw[ap]
|
| |
Out[4]=
|
-Graphics-
|
In[5]:=
|
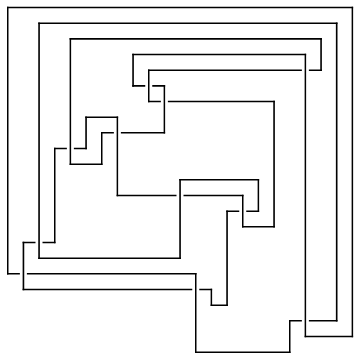
ap0 = ArcPresentation["K11n11", Reduce -> 0]
|
Out[5]=
|
ArcPresentation[{13, 19}, {20, 23}, {19, 22}, {15, 14}, {14, 2},
{1, 13}, {3, 12}, {2, 4}, {16, 18}, {17, 15}, {8, 16}, {12, 17},
{5, 7}, {4, 6}, {7, 11}, {6, 8}, {18, 10}, {11, 9}, {10, 21},
{9, 20}, {21, 5}, {22, 3}, {23, 1}]
|
| ||||
In[8]:=
|
Draw[ap0]
|
| |
Out[8]=
|
-Graphics-
|
In[9]:=
|
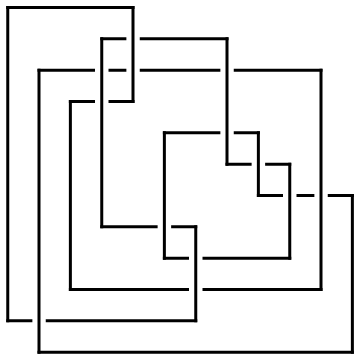
Reflect[ap_ArcPresentation] := ArcPresentation @@ (
(Last /@ Sort[Reverse /@ Position[ap, #]]) & /@ Range[Length[ap]]
)
|
In[11]:=
|
Reflect[ap] // Draw
|
| |
Out[11]=
|
-Graphics-
|
In[12]:=
|
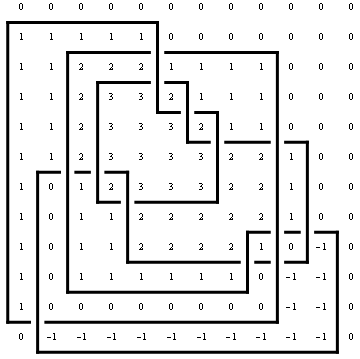
MinesweeperMatrix[ap_ArcPresentation] := Module[
{l, CurrentRow, c1, c2, k, s},
l = Length[ap];
CurrentRow = Table[0, {l}];
Table[
{c1, c2} = Sort[ap[[k]]];
s = Sign[{-1, 1}.ap[[k]]];
Do[
CurrentRow[[c]] += s,
{c, c1, c2 - 1}
];
CurrentRow,
{k, l}
]
];
|
In[14]:=
|
Draw[ap, OverlayMatrix -> MinesweeperMatrix[ap]]
|
| |
Out[14]=
|
-Graphics-
|
In[15]:=
|
{Det[t^MinesweeperMatrix[ap]], Alexander[ap][t]} // Factor
|
Out[15]=
|
11 2 2 3 4 5 6
{(-1 + t) t (1 - 5 t + 13 t - 17 t + 13 t - 5 t + t ),
2 3 4 5 6
1 - 5 t + 13 t - 17 t + 13 t - 5 t + t
-------------------------------------------}
3
t
|