Drawing Braids
(For In[1] see Setup)
In[2]:= ?BraidPlot
BraidPlot[br, opts] produces a plot of the braid br. Possible options are Mode, HTMLOpts and Images. |
Thus for example,
| In[3]:= |
br = BR[5, {{1,3}, {-2,-4}, {1, 3}}]; |
| In[4]:= |
Show[BraidPlot[br]] |
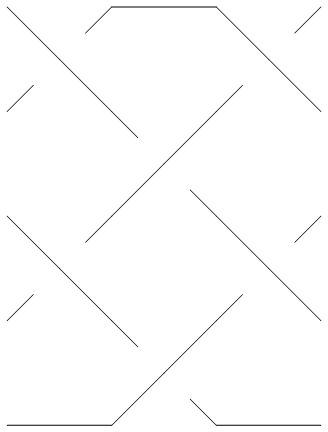
| |
| Out[4]= | -Graphics- |
BraidPlot takes several options:
| In[5]:= |
Options[BraidPlot] |
| Out[5]= | {Mode -> Graphics, Images -> {0.gif, 1.gif, 2.gif, 3.gif, 4.gif}, HTMLOpts -> }
|
The Mode option to BraidPlot defaults to "Graphics", which produces output as above. An alternative is setting Mode -> "HTML", which produces an HTML <table> that can be readily inserted into HTML documents:
| In[6]:= |
BraidPlot[br, Mode -> "HTML"] |
| Out[6]= | <table cellspacing=0 cellpadding=0 border=0> <tr><td><img src=1.gif><img src=0.gif><img src=1.gif></td></tr> <tr><td><img src=2.gif><img src=3.gif><img src=2.gif></td></tr> <tr><td><img src=1.gif><img src=4.gif><img src=1.gif></td></tr> <tr><td><img src=2.gif><img src=3.gif><img src=2.gif></td></tr> <tr><td><img src=0.gif><img src=4.gif><img src=0.gif></td></tr> </table> |
The table produced contains an array of image inclusions that together draws the braid using 5 fundamental building blocks: a horizontal "unbraided" line (0.gif above), the upper and lower halves of an overcrossing (1.gif and 2.gif above) and the upper and lower halves of an underfcrossing (3.gif and 4.gif above).
Assuming 0.gif through 4.gif are ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() , the above table is rendered as follows:
, the above table is rendered as follows:
The meaning of the Images option to BraidPlot should be clear from reading its default definition:
| In[7]:= |
Images /. Options[BraidPlot] |
| Out[7]= | {0.gif, 1.gif, 2.gif, 3.gif, 4.gif}
|
The HTMLOpts option to BraidPlot allows to insert options within the HTML <img> tags. Thus
| In[8]:= |
BraidPlot[BR[2, {1, 1}], Mode -> "HTML", HTMLOpts -> "border=1"] |
| Out[8]= | <table cellspacing=0 cellpadding=0 border=0> <tr><td><img border=1 src=1.gif><img border=1 src=1.gif></td></tr> <tr><td><img border=1 src=2.gif><img border=1 src=2.gif></td></tr> </table> |
The above table is rendered as follows:
In[9]:= ?CollapseBraid
CollapseBraid[br] groups together commuting generators in the braid br. Useful in conjunction with BraidPlot to produce compact braid plots. |
Thus compare the plots of br1 and br2 below:
| In[10]:= |
br1 = BR[TorusKnot[5, 4]] |
| Out[10]= | BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
| In[11]:= |
Show[BraidPlot[br1]] |
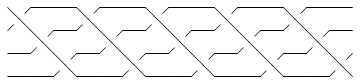
| |
| Out[11]= | -Graphics- |
| In[12]:= |
br2 = CollapseBraid[BR[TorusKnot[5, 4]]] |
| Out[12]= | BR[4, {{1}, {2}, {3, 1}, {2}, {3, 1}, {2}, {3, 1}, {2}, {3, 1}, {2}, {3}}]
|
| In[13]:= |
Show[BraidPlot[br2]] |
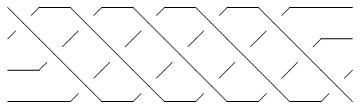
| |
| Out[13]= | -Graphics- |