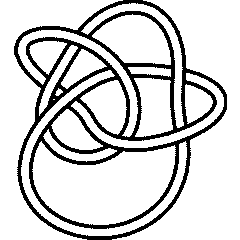
8 19
|
|
|
|
Visit 8 19's page at the Knot Server (KnotPlot driven, includes 3D interactive images!)
Visit 8 19's page at Knotilus! Visit 8 19's page at the original Knot Atlas! |
8 19 is the first non-obvious torus knot in the table - it is in fact T(4,3). It is also the pretzel knot P(3,3,-2). |
8_19 is the first non-homologically thin knot in the Rolfsen table. (That is, it's the first knot whose Khovanov homology has 'off-diagonal' elements.)
|
Knot presentations
| Planar diagram presentation | X4251 X8493 X9,15,10,14 X5,13,6,12 X13,7,14,6 X11,1,12,16 X15,11,16,10 X2837 |
| Gauss code | 1, -8, 2, -1, -4, 5, 8, -2, -3, 7, -6, 4, -5, 3, -7, 6 |
| Dowker-Thistlethwaite code | 4 8 -12 2 -14 -16 -6 -10 |
| Conway Notation | [3,3,2-] |
Three dimensional invariants
|
Four dimensional invariants
|
Polynomial invariants
| Alexander polynomial | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^3-t^2+1- t^{-2} + t^{-3} } |
| Conway polynomial | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^6+5 z^4+5 z^2+1} |
| 2nd Alexander ideal (db, data sources) | |
| Determinant and Signature | { 3, 6 } |
| Jones polynomial | |
| HOMFLY-PT polynomial (db, data sources) | |
| Kauffman polynomial (db, data sources) | |
| The A2 invariant | |
| The G2 invariant |
A1 Invariants.
| Weight | Invariant |
|---|---|
| 1 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-5} + q^{-7} + q^{-9} + q^{-11} - q^{-15} - q^{-17} } |
| 2 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-10} + q^{-12} + q^{-14} + q^{-16} + q^{-18} + q^{-20} + q^{-22} - q^{-28} - q^{-30} - q^{-32} - q^{-34} - q^{-36} + q^{-48} } |
| 3 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-15} + q^{-17} + q^{-19} + q^{-21} + q^{-23} + q^{-25} + q^{-27} + q^{-29} + q^{-31} + q^{-33} - q^{-41} - q^{-43} - q^{-45} - q^{-47} - q^{-49} - q^{-51} - q^{-53} - q^{-55} + q^{-77} + q^{-79} + q^{-81} + q^{-83} - q^{-87} - q^{-89} } |
| 4 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} + q^{-22} + q^{-24} + q^{-26} + q^{-28} + q^{-30} + q^{-32} + q^{-34} + q^{-36} + q^{-38} + q^{-40} + q^{-42} + q^{-44} - q^{-54} - q^{-56} - q^{-58} - q^{-60} - q^{-62} - q^{-64} - q^{-66} - q^{-68} - q^{-70} - q^{-72} - q^{-74} + q^{-106} + q^{-108} + q^{-110} + q^{-112} + q^{-114} + q^{-116} + q^{-118} - q^{-124} - q^{-126} - q^{-128} - q^{-130} - q^{-132} + q^{-144} } |
| 5 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-25} + q^{-27} + q^{-29} + q^{-31} + q^{-33} + q^{-35} + q^{-37} + q^{-39} + q^{-41} + q^{-43} + q^{-45} + q^{-47} + q^{-49} + q^{-51} + q^{-53} + q^{-55} - q^{-67} - q^{-69} - q^{-71} - q^{-73} - q^{-75} - q^{-77} - q^{-79} - q^{-81} - q^{-83} - q^{-85} - q^{-87} - q^{-89} - q^{-91} - q^{-93} + q^{-135} + q^{-137} + q^{-139} + q^{-141} + q^{-143} + q^{-145} + q^{-147} + q^{-149} + q^{-151} + q^{-153} - q^{-161} - q^{-163} - q^{-165} - q^{-167} - q^{-169} - q^{-171} - q^{-173} - q^{-175} + q^{-197} + q^{-199} + q^{-201} + q^{-203} - q^{-207} - q^{-209} } |
| 6 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-30} + q^{-32} + q^{-34} + q^{-36} + q^{-38} + q^{-40} + q^{-42} + q^{-44} + q^{-46} + q^{-48} + q^{-50} + q^{-52} + q^{-54} + q^{-56} + q^{-58} + q^{-60} + q^{-62} + q^{-64} + q^{-66} - q^{-80} - q^{-82} - q^{-84} - q^{-86} - q^{-88} - q^{-90} - q^{-92} - q^{-94} - q^{-96} - q^{-98} - q^{-100} - q^{-102} - q^{-104} - q^{-106} - q^{-108} - q^{-110} - q^{-112} + q^{-164} + q^{-166} + q^{-168} + q^{-170} + q^{-172} + q^{-174} + q^{-176} + q^{-178} + q^{-180} + q^{-182} + q^{-184} + q^{-186} + q^{-188} - q^{-198} - q^{-200} - q^{-202} - q^{-204} - q^{-206} - q^{-208} - q^{-210} - q^{-212} - q^{-214} - q^{-216} - q^{-218} + q^{-250} + q^{-252} + q^{-254} + q^{-256} + q^{-258} + q^{-260} + q^{-262} - q^{-268} - q^{-270} - q^{-272} - q^{-274} - q^{-276} + q^{-288} } |
A2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-10} + q^{-12} +2 q^{-14} +2 q^{-16} +2 q^{-18} - q^{-22} -2 q^{-24} -2 q^{-26} - q^{-28} + q^{-32} } |
| 1,1 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} +2 q^{-22} +4 q^{-24} +6 q^{-26} +7 q^{-28} +6 q^{-30} +4 q^{-32} +2 q^{-34} - q^{-36} -4 q^{-38} -6 q^{-40} -8 q^{-42} -7 q^{-44} -6 q^{-46} -4 q^{-48} +2 q^{-52} +4 q^{-54} +4 q^{-56} +4 q^{-58} + q^{-60} -2 q^{-64} -2 q^{-66} - q^{-68} +2 q^{-72} } |
| 2,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} + q^{-22} +2 q^{-24} +2 q^{-26} +3 q^{-28} +3 q^{-30} +4 q^{-32} +3 q^{-34} +3 q^{-36} + q^{-38} -2 q^{-42} -3 q^{-44} -5 q^{-46} -5 q^{-48} -5 q^{-50} -4 q^{-52} -3 q^{-54} -2 q^{-56} + q^{-58} +2 q^{-60} +4 q^{-62} +4 q^{-64} +4 q^{-66} + q^{-68} -2 q^{-72} -2 q^{-74} - q^{-76} + q^{-80} } |
A3 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} + q^{-22} +3 q^{-24} +4 q^{-26} +6 q^{-28} +5 q^{-30} +5 q^{-32} + q^{-34} -2 q^{-36} -6 q^{-38} -7 q^{-40} -7 q^{-42} -5 q^{-44} - q^{-46} + q^{-48} +3 q^{-50} +2 q^{-52} +2 q^{-54} } |
| 1,0,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-15} + q^{-17} +2 q^{-19} +3 q^{-21} +3 q^{-23} +2 q^{-25} + q^{-27} - q^{-29} -3 q^{-31} -3 q^{-33} -3 q^{-35} - q^{-37} + q^{-41} + q^{-43} } |
| 1,0,1 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-30} +2 q^{-32} +5 q^{-34} +9 q^{-36} +14 q^{-38} +17 q^{-40} +19 q^{-42} +16 q^{-44} +9 q^{-46} -10 q^{-50} -19 q^{-52} -25 q^{-54} -27 q^{-56} -23 q^{-58} -16 q^{-60} -7 q^{-62} +3 q^{-64} +9 q^{-66} +15 q^{-68} +15 q^{-70} +11 q^{-72} +7 q^{-74} +2 q^{-76} -2 q^{-78} -4 q^{-80} -3 q^{-82} -3 q^{-84} - q^{-86} - q^{-88} +2 q^{-96} } |
A4 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-30} + q^{-32} +3 q^{-34} +5 q^{-36} +8 q^{-38} +9 q^{-40} +12 q^{-42} +10 q^{-44} +8 q^{-46} +2 q^{-48} -4 q^{-50} -11 q^{-52} -15 q^{-54} -17 q^{-56} -15 q^{-58} -10 q^{-60} -5 q^{-62} +2 q^{-64} +5 q^{-66} +8 q^{-68} +7 q^{-70} +6 q^{-72} +3 q^{-74} + q^{-76} - q^{-78} - q^{-80} - q^{-82} - q^{-84} } |
| 1,0,0,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} + q^{-22} +2 q^{-24} +3 q^{-26} +4 q^{-28} +3 q^{-30} +3 q^{-32} + q^{-34} - q^{-36} -3 q^{-38} -4 q^{-40} -4 q^{-42} -3 q^{-44} - q^{-46} + q^{-50} + q^{-52} + q^{-54} } |
B2 Invariants.
| Weight | Invariant |
|---|---|
| 0,1 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-20} + q^{-22} + q^{-24} +2 q^{-26} +2 q^{-28} + q^{-30} + q^{-32} + q^{-34} - q^{-40} - q^{-42} - q^{-44} - q^{-46} - q^{-48} - q^{-50} } |
| 1,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-30} + q^{-34} + q^{-36} +2 q^{-38} + q^{-40} +3 q^{-42} +2 q^{-44} +3 q^{-46} +2 q^{-48} +2 q^{-50} + q^{-52} + q^{-54} - q^{-56} - q^{-58} -2 q^{-60} -3 q^{-62} -3 q^{-64} -3 q^{-66} -3 q^{-68} -3 q^{-70} - q^{-72} - q^{-74} +2 q^{-80} + q^{-82} + q^{-84} + q^{-86} + q^{-88} } |
D4 Invariants.
| Weight | Invariant |
|---|---|
| 1,0,0,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-30} + q^{-32} +2 q^{-34} +4 q^{-36} +5 q^{-38} +6 q^{-40} +7 q^{-42} +6 q^{-44} +4 q^{-46} +2 q^{-48} -2 q^{-50} -5 q^{-52} -7 q^{-54} -8 q^{-56} -8 q^{-58} -6 q^{-60} -4 q^{-62} - q^{-64} + q^{-66} +2 q^{-68} +3 q^{-70} +2 q^{-72} +2 q^{-74} + q^{-76} } |
G2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^{-50} + q^{-52} + q^{-54} + q^{-56} + q^{-58} + q^{-60} +2 q^{-62} +2 q^{-64} + q^{-66} + q^{-68} +2 q^{-70} +2 q^{-72} +2 q^{-74} + q^{-76} + q^{-80} +2 q^{-82} - q^{-94} -2 q^{-96} - q^{-98} - q^{-100} -2 q^{-102} -2 q^{-104} -2 q^{-106} - q^{-108} - q^{-110} -2 q^{-112} -2 q^{-114} - q^{-116} - q^{-122} - q^{-124} + q^{-126} + q^{-128} + q^{-136} + q^{-138} + q^{-144} } |
.
KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of August 31, 2006, 11:25:27.5625.
|
In[3]:=
|
K = Knot["8 19"];
|
In[4]:=
|
Alexander[K][t]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^3-t^2+1- t^{-2} + t^{-3} } |
In[5]:=
|
Conway[K][z]
|
Out[5]=
|
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^6+5 z^4+5 z^2+1} |
In[6]:=
|
Alexander[K, 2][t]
|
KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.
|
Out[6]=
|
In[7]:=
|
{KnotDet[K], KnotSignature[K]}
|
Out[7]=
|
{ 3, 6 } |
In[8]:=
|
Jones[K][q]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[8]=
|
In[9]:=
|
HOMFLYPT[K][a, z]
|
KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.
|
Out[9]=
|
In[10]:=
|
Kauffman[K][a, z]
|
KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.
|
Out[10]=
|
Vassiliev invariants
| V2 and V3: | (5, 10) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
The coefficients of the monomials Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^rq^j} are shown, along with their alternating sums Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} (fixed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , alternation over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} ). The squares with yellow highlighting are those on the "critical diagonals", where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j-2r=s+1} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j-2r=s+1} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=} 6 is the signature of 8 19. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.
|
0 | 1 | 2 | 3 | 4 | 5 | χ | |||||||||
| 17 | 1 | -1 | ||||||||||||||
| 15 | 1 | -1 | ||||||||||||||
| 13 | 1 | 1 | 0 | |||||||||||||
| 11 | 1 | 1 | ||||||||||||||
| 9 | 1 | 1 | ||||||||||||||
| 7 | 1 | 1 | ||||||||||||||
| 5 | 1 | 1 |
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textrm{Include}(\textrm{ColouredJonesM.mhtml})}
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 17, 2005, 14:44:34)... | |
In[2]:= | Crossings[Knot[8, 19]] |
Out[2]= | 8 |
In[3]:= | PD[Knot[8, 19]] |
Out[3]= | PD[X[4, 2, 5, 1], X[8, 4, 9, 3], X[9, 15, 10, 14], X[5, 13, 6, 12], X[13, 7, 14, 6], X[11, 1, 12, 16], X[15, 11, 16, 10], X[2, 8, 3, 7]] |
In[4]:= | GaussCode[Knot[8, 19]] |
Out[4]= | GaussCode[1, -8, 2, -1, -4, 5, 8, -2, -3, 7, -6, 4, -5, 3, -7, 6] |
In[5]:= | BR[Knot[8, 19]] |
Out[5]= | BR[3, {1, 1, 1, 2, 1, 1, 1, 2}] |
In[6]:= | alex = Alexander[Knot[8, 19]][t] |
Out[6]= | -3 -2 2 3 1 + t - t - t + t |
In[7]:= | Conway[Knot[8, 19]][z] |
Out[7]= | 2 4 6 1 + 5 z + 5 z + z |
In[8]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[8]= | {Knot[8, 19]} |
In[9]:= | {KnotDet[Knot[8, 19]], KnotSignature[Knot[8, 19]]} |
Out[9]= | {3, 6} |
In[10]:= | J=Jones[Knot[8, 19]][q] |
Out[10]= | 3 5 8 q + q - q |
In[11]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[11]= | {Knot[8, 19]} |
In[12]:= | A2Invariant[Knot[8, 19]][q] |
Out[12]= | 10 12 14 16 18 22 24 26 28 32 q + q + 2 q + 2 q + 2 q - q - 2 q - 2 q - q + q |
In[13]:= | Kauffman[Knot[8, 19]][a, z] |
Out[13]= | 2 2 3 3 4-10 5 5 5 z 5 z 10 z 10 z 5 z 5 z 6 z |
In[14]:= | {Vassiliev[2][Knot[8, 19]], Vassiliev[3][Knot[8, 19]]} |
Out[14]= | {0, 10} |
In[15]:= | Kh[Knot[8, 19]][q, t] |
Out[15]= | 5 7 9 2 13 3 11 4 13 4 15 5 17 5 q + q + q t + q t + q t + q t + q t + q t |