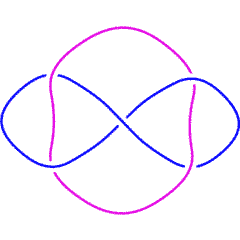
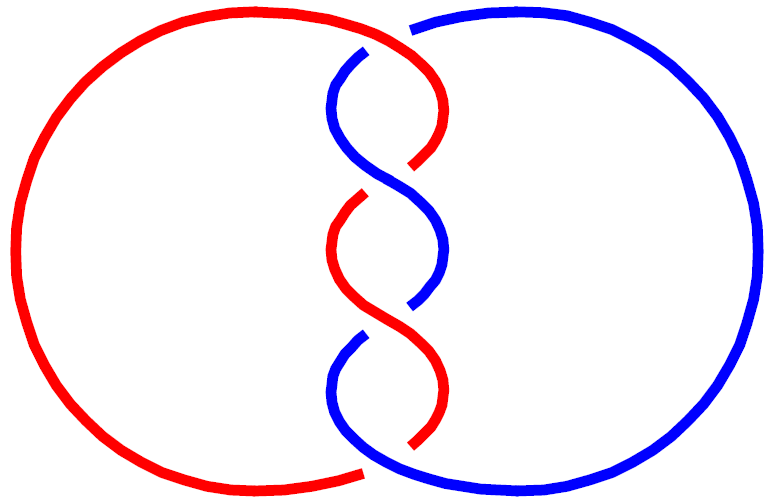
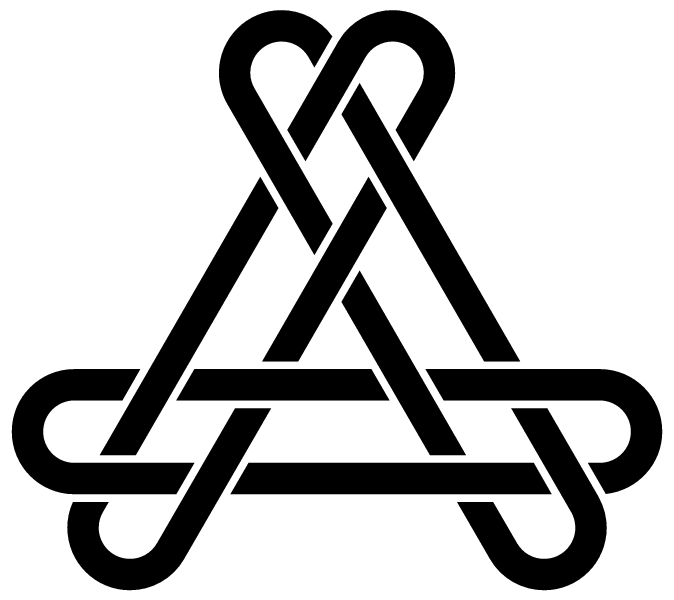
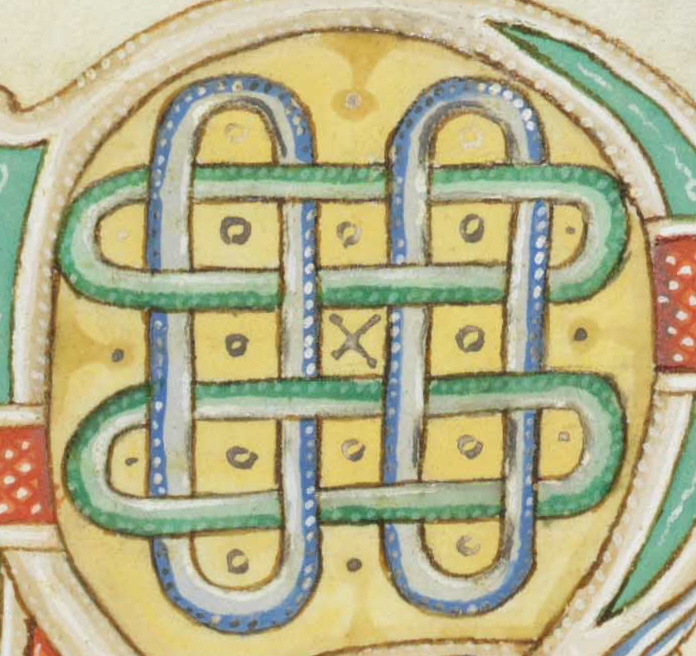
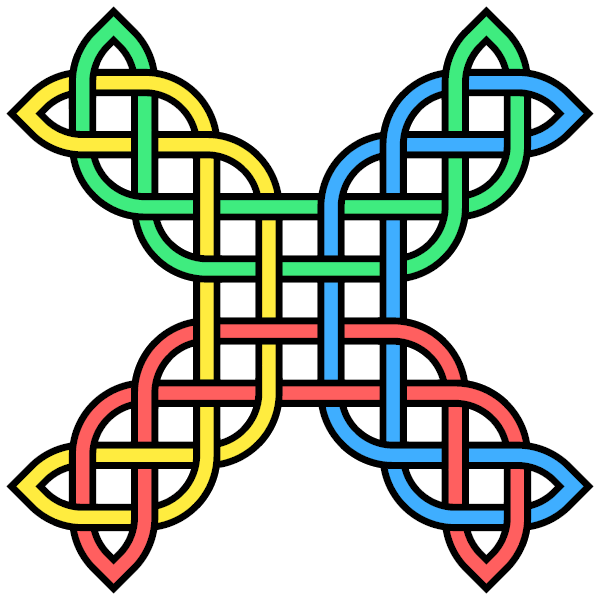
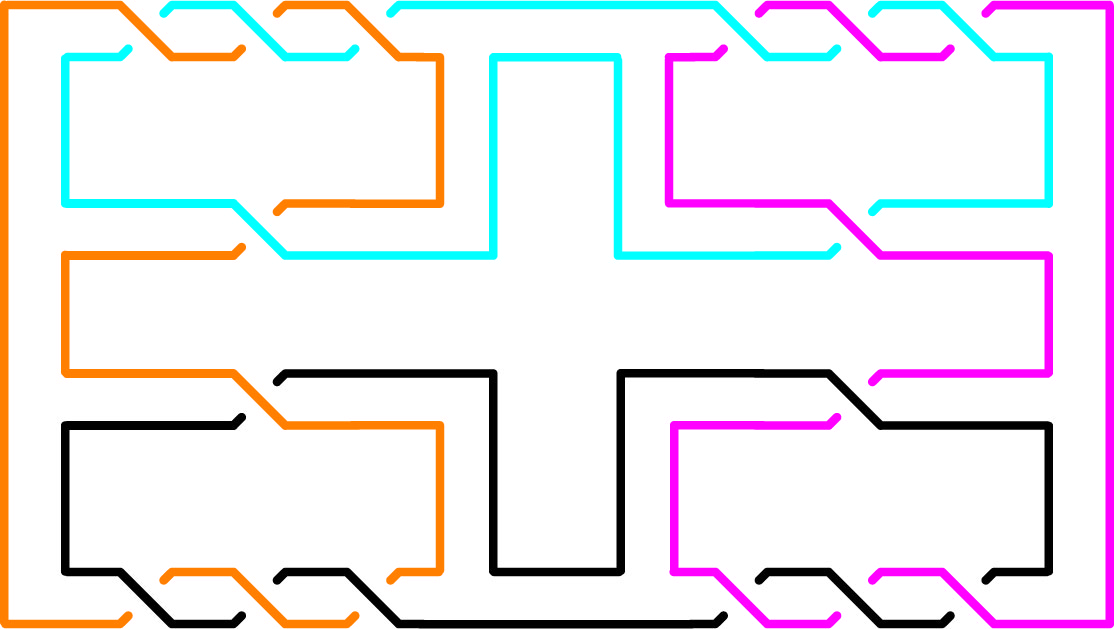
L4a1

L2a1

L5a1

	Visit L4a1's page at Knotilus! Visit L4a1's page at the original Knot Atlas!
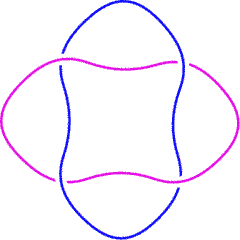
	L4a1 is $4_{1}^{2}$ in the Rolfsen table of links. It frequently occurs in late Roman mosaics and some medieval decorations. In this context, it is called the "Solomon's knot" (sigillum Salomonis) or "guilloche knot". It is also the "Kramo-bone" symbol (meaning "one being bad makes all appear to be bad") of the Adinkra symbol system. Link L10a101 contains multiple L4a1 configurations.

Simple squared depiction		A Kolam with two cycles[1]		Hearst Castle tile [2]		Mosaic seen at Kibbutz Lahav [3]
Carving above door of church in Italy		Decorative depiction		(crossings along one side)		Linked hearts used as symbol of Vendée region of France
Heraldic ornament.		Composed of intersecting circles.		Decorative fitting closely within square.		Ancient Roman mosaic.
Made of two (impossible) Penrose rectangles.		Array of "Solomon's knots" forming overall circular patterns.		Configuration of three L4a1		Configuration of four L4a1
Medieval manuscript		Medieval manuscript		Medieval manuscript		Rotated knotwork cross with eight L4a1 sub-configurations
Knotopologynn-diagram for "Solomon's knots"		Commercial logo

Knot presentations

Planar diagram presentation	X6172 X8354 X2536 X4718
Gauss code	{1, -3, 2, -4}, {3, -1, 4, -2}

Polynomial invariants

Multivariable Alexander Polynomial (in $u$, $v$, $w$, ...)	${\frac {-u-v}{{\sqrt {u}}{\sqrt {v}}}}$ (db)
Jones polynomial	$-{\frac {1}{q^{9/2}}}-{\frac {1}{q^{5/2}}}+{\frac {1}{q^{3/2}}}-{\frac {1}{\sqrt {q}}}$ (db)
Signature	-1 (db)
HOMFLY-PT polynomial	$a^{5}z^{-1}-a^{3}z-a^{3}z^{-1}-az$ (db)
Kauffman polynomial	$a^{5}z^{3}-3a^{5}z+a^{5}z^{-1}+a^{4}z^{2}-a^{4}+a^{3}z^{3}-2a^{3}z+a^{3}z^{-1}+a^{2}z^{2}+az$ (db)

Vassiliev invariants

V2 and V3:

(0, $-{\frac {65}{24}}$)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 Data:L4a1/V 2,1 Data:L4a1/V 3,1 Data:L4a1/V 4,1 Data:L4a1/V 4,2 Data:L4a1/V 4,3 Data:L4a1/V 5,1 Data:L4a1/V 5,2 Data:L4a1/V 5,3 Data:L4a1/V 5,4 Data:L4a1/V 6,1 Data:L4a1/V 6,2 Data:L4a1/V 6,3 Data:L4a1/V 6,4 Data:L4a1/V 6,5 Data:L4a1/V 6,6 Data:L4a1/V 6,7 Data:L4a1/V 6,8 Data:L4a1/V 6,9

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$-1 is the signature of L4a1. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ -4 -3 -2 -1 0 χ 0         1 1 -2       1 1 0 -4           0 -6     1     1 -8 1         1 -10 1         1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=-2$ $i=0$ $r=-4$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=-3$ $r=-2$ ${\mathbb {Z} }$ $r=-1$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=0$ ${\mathbb {Z} }$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

${\textrm {Include}}({\textrm {ColouredJonesM.mhtml}})$

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 17, 2005, 14:44:34)...
In[2]:=	Crossings[Link[4, Alternating, 1]]
Out[2]=	4
In[3]:=	PD[Link[4, Alternating, 1]]
Out[3]=	PD[X[6, 1, 7, 2], X[8, 3, 5, 4], X[2, 5, 3, 6], X[4, 7, 1, 8]]
In[4]:=	GaussCode[Link[4, Alternating, 1]]
Out[4]=	GaussCode[{1, -3, 2, -4}, {3, -1, 4, -2}]
In[5]:=	BR[Link[4, Alternating, 1]]
Out[5]=	BR[Link[4, Alternating, 1]]
In[6]:=	alex = Alexander[Link[4, Alternating, 1]][t]
Out[6]=	ComplexInfinity
In[7]:=	Conway[Link[4, Alternating, 1]][z]
Out[7]=	ComplexInfinity
In[8]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[8]=	{}
In[9]:=	{KnotDet[Link[4, Alternating, 1]], KnotSignature[Link[4, Alternating, 1]]}
Out[9]=	{Infinity, -1}
In[10]:=	J=Jones[Link[4, Alternating, 1]][q]
Out[10]=	-(9/2) -(5/2) -(3/2) 1 -q - q + q - ------- Sqrt[q]
In[11]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[11]=	{}
In[12]:=	A2Invariant[Link[4, Alternating, 1]][q]
Out[12]=	-16 2 2 2 -8 1 + q + --- + --- + --- + q 14 12 10 q q q
In[13]:=	Kauffman[Link[4, Alternating, 1]][a, z]
Out[13]=	3 5 4 a a 3 5 2 2 4 2 3 3 5 3 a - -- - -- - a z + 2 a z + 3 a z - a z - a z - a z - a z z z
In[14]:=	{Vassiliev[2][Link[4, Alternating, 1]], Vassiliev[3][Link[4, Alternating, 1]]}
Out[14]=	65 {0, -(--)} 24
In[15]:=	Kh[Link[4, Alternating, 1]][q, t]
Out[15]=	-2 1 1 1 1 1 + q + ------ + ----- + ----- + ---- 10 4 8 4 6 2 2 q t q t q t q t