[http://s1.shard.jp/olharder/automotive-executive.html wal mart auto service center
] unistalling norton antivirus [http://s1.shard.jp/galeach/new12.html asian scene girl
] [http://s1.shard.jp/olharder/auto-insurance.html autoexec express
] [http://s1.shard.jp/losaul/online-clothing.html diggers australia pty ltd
] [http://s1.shard.jp/olharder/stan-olsen-auto.html pip auto
] url [http://s1.shard.jp/olharder/napa-auto-parts.html auto site trader uk
] [http://s1.shard.jp/olharder/chery-automobile.html duplicate automobile title
] [http://s1.shard.jp/bireba/download-symantec.html avg free antivirus review
] [http://s1.shard.jp/galeach/new173.html asian gang shooting
] alerta antivirus.es [http://s1.shard.jp/bireba/mc-afee-antivirus.html good antivirus programs
] index antivirus2003 [http://s1.shard.jp/losaul/newcastle-australia.html griffith university brisbane australia
] [http://s1.shard.jp/bireba/grisoft-antivirus.html panda titanium 2006 antivirus crack
] used automobile louisville [http://s1.shard.jp/bireba/the-symantec-antivirus.html server2003 antivirus
] [http://s1.shard.jp/losaul/1999-australian.html husqvarna sewing machines australia
] [http://s1.shard.jp/losaul/alice-springs.html australian art gallery sydney
] [http://s1.shard.jp/olharder/jl-french-automotive.html auto body college repair state
] [http://s1.shard.jp/olharder/automation-expense.html united automobile insurance company illinois
] [http://s1.shard.jp/frhorton/k7b9qt4bf.html africa airline onetime south
] top [http://s1.shard.jp/olharder/auto-emissions-test.html insurance automobile
] [http://s1.shard.jp/frhorton/w2yqtuc7f.html east african community of orange county
] [http://s1.shard.jp/losaul/tenders-australian.html average weekly earnings australia
] [http://s1.shard.jp/frhorton/1aei449pv.html africa business forum
] [http://s1.shard.jp/galeach/new146.html euthanasia views
] [http://s1.shard.jp/bireba/extendia-antivirus.html antivirus software for pc
] [http://s1.shard.jp/losaul/emmigrating-australia.html australian animal print
] [http://s1.shard.jp/frhorton/lr43ii5kv.html african american proverb
] [http://s1.shard.jp/galeach/new68.html disneychannel asia
] index [http://s1.shard.jp/bireba/antivirus-checking.html norton antivirus definitions disk
] [http://s1.shard.jp/frhorton/lyfh4c7mt.html africa car luxury rental south
] [http://s1.shard.jp/bireba/download-norton.html types of antivirus software
] [http://s1.shard.jp/bireba/symantec-antivirus.html norman antivirus download
] download norton antivirus 2004 full version [http://s1.shard.jp/galeach/new196.html optasia electronics
] [http://s1.shard.jp/bireba/antivirus-trials.html installing antivirus software
] african ancestry dna testing [http://s1.shard.jp/bireba/review-zone-alarm.html tim oleary australian antivirus
] [http://s1.shard.jp/olharder/download-autoroute.html auto arrange desktop icons
] [http://s1.shard.jp/galeach/new119.html asian tsunami blogs
] [http://s1.shard.jp/losaul/time-difference.html look bikes australia
] [http://s1.shard.jp/bireba/panda-free-antivirus.html download free norton antivirus software
] [http://s1.shard.jp/galeach/new130.html lyrics to fantasia barrino
] interfund south africa
http://www.textpaslisi.com
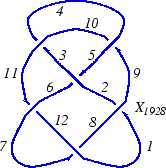
The PD notation
In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols  where
where  ,
,  ,
,  and
and  are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the
are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot above is:

(This of course is the Miller Institute knot, the mirror image of the knot 6_2)
(For In[1] see Setup)
| In[1]:=
|
?PD
|
| PD[v1, v2, ...] represents a planar diagram whose vertices are v1, v2, .... PD also acts as a "type caster", so for example, PD[K] where K is is a named knot (or link) returns the PD presentation of that knot.
|
|
| In[2]:=
|
PD::about
|
| The PD to GaussCode and to MorseLink conversions were written by Siddarth Sankaran at the University of Toronto in the summer of 2005.
|
|
| In[3]:=
|
?X
|
| X[i,j,k,l] represents a crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counterclockwise through j, k and l. The (sometimes ambiguous) orientation of the upper strand is determined by the ordering of {j,l}.
|
|
Thus, for example, let us compute the determinant of the above knot:
In[4]:=
|
K = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,12], X[9,4,10,5], X[11,7,12,6]
];
|
In[5]:=
|
Alexander[K][-1]
|
Out[5]=
|
-11
|
Some further details
| In[6]:=
|
?Xp
|
| Xp[i,j,k,l] represents a positive (right handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from l to j regardless of the ordering of {j,l}. Presently Xp is only lightly supported.
|
|
| In[7]:=
|
?Xm
|
| Xm[i,j,k,l] represents a negative (left handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from j to l regardless of the ordering of {j,l}. Presently Xm is only lightly supported.
|
|
| In[8]:=
|
?P
|
| P[i,j] represents a bivalent vertex whose adjacent edges are i and j (i.e., a "Point" between the segment i and the segment j). Presently P is only lightly supported.
|
|
For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13:
In[9]:=
|
K1 = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,13], X[9,4,10,5], X[11,7,12,6],
P[12,13]
];
|
At the moment, many of our routines do not know to ignore such "extra points". But some do:
In[10]:=
|
Jones[K][q] == Jones[K1][q]
|
Out[10]=
|
True
|
| In[11]:=
|
?Loop
|
| Loop[i] represents a crossingsless loop labeled i.
|
|
Hence we can verify that the A2 invariant of the unknot is  :
:
In[12]:=
|
A2Invariant[Loop[1]][q]
|
Out[12]=
|
-2 2
1 + q + q
|







