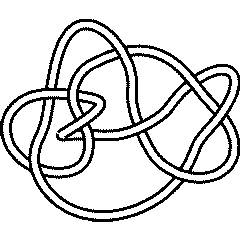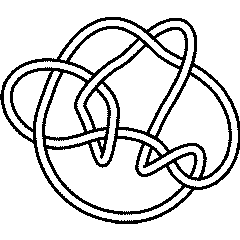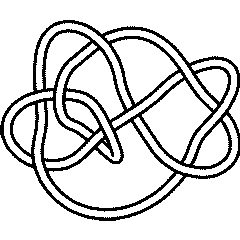10 52

10_51

10_53

(KnotPlot image)

See the full Rolfsen Knot Table.

Visit 10 52's page at the Knot Server (KnotPlot driven, includes 3D interactive images!)

Visit 10 52 at Knotilus!

[edit 10 52 Quick Notes]

[edit 10 52 Further Notes and Views]

Knot presentations

Planar diagram presentation	X₆₂₇₁ X₈₄₉₃ X_14,6,15,5 X_20,15,1,16 X_16,9,17,10 X_10,19,11,20 X_18,11,19,12 X_12,17,13,18 X₂₈₃₇ X_4,14,5,13
Gauss code	1, -9, 2, -10, 3, -1, 9, -2, 5, -6, 7, -8, 10, -3, 4, -5, 8, -7, 6, -4
Dowker-Thistlethwaite code	6 8 14 2 16 18 4 20 12 10
Conway Notation	[311,3,2]

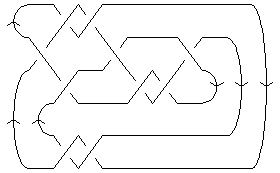
Minimum Braid Representative

A Morse Link Presentation

An Arc Presentation

Length is 11, width is 4,

Braid index is 4

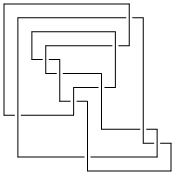
[{7, 13}, {2, 12}, {13, 11}, {12, 8}, {1, 6}, {5, 7}, {6, 9}, {8, 4}, {3, 5}, {4, 10}, {9, 3}, {11, 2}, {10, 1}]

[edit Notes on presentations of 10 52]

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:= AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091.

Read more at http://katlas.org/wiki/KnotTheory.

In[3]:= K = Knot["10 52"];

In[4]:= PD[K]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]= X₆₂₇₁ X₈₄₉₃ X_14,6,15,5 X_20,15,1,16 X_16,9,17,10 X_10,19,11,20 X_18,11,19,12 X_12,17,13,18 X₂₈₃₇ X_4,14,5,13

In[5]:= GaussCode[K]

Out[5]= 1, -9, 2, -10, 3, -1, 9, -2, 5, -6, 7, -8, 10, -3, 4, -5, 8, -7, 6, -4

In[6]:= DTCode[K]

Out[6]= 6 8 14 2 16 18 4 20 12 10

(The path below may be different on your system)

In[7]:= AppendTo[$Path, "C:/bin/LinKnot/"];

In[8]:= ConwayNotation[K]

Out[8]= [311,3,2]

In[9]:= br = BR[K]

KnotTheory::credits: The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See arXiv:math.GT/0401051.

Out[9]= ${\textrm {BR}}(4,\{1,1,1,-2,1,1,-2,-2,-3,2,-3\})$

In[10]:= {First[br], Crossings[br], BraidIndex[K]}

KnotTheory::credits: The braid index data known to KnotTheory` is taken from Charles Livingston's http://www.indiana.edu/~knotinfo/.

KnotTheory::loading: Loading precomputed data in IndianaData`.

Out[10]= { 4, 11, 4 }

In[11]:= Show[BraidPlot[br]]

Out[11]= -Graphics-

In[12]:= Show[DrawMorseLink[K]]

KnotTheory::credits: "MorseLink was added to KnotTheory` by Siddarth Sankaran at the University of Toronto in the summer of 2005."

KnotTheory::credits: "DrawMorseLink was written by Siddarth Sankaran at the University of Toronto in the summer of 2005."

Out[12]= -Graphics-

In[13]:= ap = ArcPresentation[K]

Out[13]= ArcPresentation[{7, 13}, {2, 12}, {13, 11}, {12, 8}, {1, 6}, {5, 7}, {6, 9}, {8, 4}, {3, 5}, {4, 10}, {9, 3}, {11, 2}, {10, 1}]

In[14]:= Draw[ap]

Out[14]= -Graphics-

Three dimensional invariants

Symmetry type	Reversible
Unknotting number	2
3-genus	3
Bridge index	3
Super bridge index	Missing
Nakanishi index	1
Maximal Thurston-Bennequin number	[-4][-8]
Hyperbolic Volume	11.5375
A-Polynomial	See Data:10 52/A-polynomial

[edit Notes for 10 52's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus	$1$
Topological 4 genus	$1$
Concordance genus	$3$
Rasmussen s-Invariant	-2

[edit Notes for 10 52's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$2t^{3}-7t^{2}+13t-15+13t^{-1}-7t^{-2}+2t^{-3}$
Conway polynomial	$2z^{6}+5z^{4}+3z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 59, 2 }
Jones polynomial	$-q^{6}+3q^{5}-6q^{4}+8q^{3}-9q^{2}+10q-8+7q^{-1}-4q^{-2}+2q^{-3}-q^{-4}$
HOMFLY-PT polynomial (db, data sources)	$z^{6}a^{-2}+z^{6}-a^{2}z^{4}+3z^{4}a^{-2}-z^{4}a^{-4}+4z^{4}-3a^{2}z^{2}+2z^{2}a^{-2}-2z^{2}a^{-4}+6z^{2}-2a^{2}-a^{-4}+4$
Kauffman polynomial (db, data sources)	$az^{9}+z^{9}a^{-1}+2a^{2}z^{8}+4z^{8}a^{-2}+6z^{8}+a^{3}z^{7}+az^{7}+7z^{7}a^{-1}+7z^{7}a^{-3}-9a^{2}z^{6}-3z^{6}a^{-2}+8z^{6}a^{-4}-20z^{6}-5a^{3}z^{5}-16az^{5}-28z^{5}a^{-1}-11z^{5}a^{-3}+6z^{5}a^{-5}+13a^{2}z^{4}-9z^{4}a^{-2}-12z^{4}a^{-4}+3z^{4}a^{-6}+19z^{4}+8a^{3}z^{3}+24az^{3}+24z^{3}a^{-1}+2z^{3}a^{-3}-5z^{3}a^{-5}+z^{3}a^{-7}-7a^{2}z^{2}+4z^{2}a^{-2}+6z^{2}a^{-4}-9z^{2}-4a^{3}z-9az-7za^{-1}+2za^{-5}+2a^{2}-a^{-4}+4$
The A2 invariant	$-q^{12}-q^{8}-q^{6}+2q^{4}+3+2q^{-2}+2q^{-6}-2q^{-8}+q^{-10}-q^{-12}-q^{-14}+q^{-16}-q^{-18}$
The G2 invariant	$q^{60}-q^{58}+4q^{56}-6q^{54}+6q^{52}-6q^{50}-q^{48}+12q^{46}-25q^{44}+33q^{42}-31q^{40}+12q^{38}+14q^{36}-46q^{34}+64q^{32}-64q^{30}+38q^{28}-46q^{24}+71q^{22}-71q^{20}+46q^{18}-4q^{16}-32q^{14}+53q^{12}-47q^{10}+21q^{8}+18q^{6}-42q^{4}+56q^{2}-36+2q^{-2}+45q^{-4}-75q^{-6}+88q^{-8}-62q^{-10}+17q^{-12}+40q^{-14}-83q^{-16}+100q^{-18}-82q^{-20}+39q^{-22}+15q^{-24}-58q^{-26}+72q^{-28}-57q^{-30}+21q^{-32}+17q^{-34}-41q^{-36}+39q^{-38}-19q^{-40}-13q^{-42}+38q^{-44}-48q^{-46}+40q^{-48}-15q^{-50}-17q^{-52}+41q^{-54}-55q^{-56}+50q^{-58}-32q^{-60}+8q^{-62}+15q^{-64}-33q^{-66}+39q^{-68}-36q^{-70}+26q^{-72}-9q^{-74}-5q^{-76}+12q^{-78}-18q^{-80}+16q^{-82}-12q^{-84}+8q^{-86}-q^{-88}-2q^{-90}+3q^{-92}-4q^{-94}+3q^{-96}-2q^{-98}+q^{-100}$

Further Quantum Invariants

Further quantum knot invariants for 10_52.

A1 Invariants.

Weight	Invariant
1	$-q^{9}+q^{7}-2q^{5}+3q^{3}-q+2q^{-1}+q^{-3}-q^{-5}+2q^{-7}-3q^{-9}+2q^{-11}-q^{-13}$
2	$q^{28}-q^{26}-2q^{24}+4q^{22}-8q^{18}+6q^{16}+6q^{14}-13q^{12}+3q^{10}+12q^{8}-12q^{6}-3q^{4}+14q^{2}-4-7q^{-2}+8q^{-4}+5q^{-6}-8q^{-8}-2q^{-10}+11q^{-12}-2q^{-14}-12q^{-16}+11q^{-18}+3q^{-20}-14q^{-22}+8q^{-24}+3q^{-26}-8q^{-28}+4q^{-30}+q^{-32}-2q^{-34}+q^{-36}$
3	$-q^{57}+q^{55}+2q^{53}-5q^{49}-2q^{47}+8q^{45}+8q^{43}-10q^{41}-17q^{39}+6q^{37}+28q^{35}+4q^{33}-35q^{31}-20q^{29}+33q^{27}+38q^{25}-26q^{23}-49q^{21}+8q^{19}+57q^{17}+7q^{15}-54q^{13}-24q^{11}+50q^{9}+36q^{7}-37q^{5}-47q^{3}+28q+52q^{-1}-13q^{-3}-56q^{-5}+57q^{-9}+14q^{-11}-46q^{-13}-29q^{-15}+35q^{-17}+41q^{-19}-12q^{-21}-50q^{-23}-8q^{-25}+46q^{-27}+30q^{-29}-43q^{-31}-41q^{-33}+30q^{-35}+43q^{-37}-21q^{-39}-36q^{-41}+14q^{-43}+25q^{-45}-9q^{-47}-18q^{-49}+8q^{-51}+10q^{-53}-6q^{-55}-3q^{-57}+3q^{-59}+2q^{-61}-2q^{-63}-q^{-65}+2q^{-67}-q^{-69}$
4	$q^{96}-q^{94}-2q^{92}+q^{88}+7q^{86}-8q^{82}-8q^{80}-6q^{78}+22q^{76}+20q^{74}-3q^{72}-28q^{70}-48q^{68}+14q^{66}+56q^{64}+58q^{62}-2q^{60}-110q^{58}-73q^{56}+19q^{54}+133q^{52}+128q^{50}-68q^{48}-163q^{46}-145q^{44}+71q^{42}+247q^{40}+114q^{38}-88q^{36}-278q^{34}-136q^{32}+180q^{30}+256q^{28}+125q^{26}-222q^{24}-289q^{22}-21q^{20}+223q^{18}+284q^{16}-48q^{14}-286q^{12}-180q^{10}+103q^{8}+313q^{6}+86q^{4}-214q^{2}-243+15q^{-2}+287q^{-4}+157q^{-6}-158q^{-8}-277q^{-10}-41q^{-12}+253q^{-14}+224q^{-16}-74q^{-18}-288q^{-20}-139q^{-22}+143q^{-24}+280q^{-26}+98q^{-28}-196q^{-30}-245q^{-32}-92q^{-34}+212q^{-36}+282q^{-38}+40q^{-40}-222q^{-42}-320q^{-44}+10q^{-46}+303q^{-48}+245q^{-50}-51q^{-52}-350q^{-54}-156q^{-56}+162q^{-58}+248q^{-60}+82q^{-62}-213q^{-64}-146q^{-66}+40q^{-68}+124q^{-70}+84q^{-72}-91q^{-74}-60q^{-76}+11q^{-78}+34q^{-80}+36q^{-82}-39q^{-84}-10q^{-86}+8q^{-88}+3q^{-90}+13q^{-92}-15q^{-94}+q^{-96}+4q^{-98}-3q^{-100}+3q^{-102}-4q^{-104}+2q^{-106}+q^{-108}-2q^{-110}+q^{-112}$
5	$-q^{145}+q^{143}+2q^{141}-q^{137}-3q^{135}-5q^{133}+10q^{129}+10q^{127}+3q^{125}-8q^{123}-24q^{121}-23q^{119}+6q^{117}+40q^{115}+50q^{113}+24q^{111}-38q^{109}-96q^{107}-86q^{105}+2q^{103}+120q^{101}+175q^{99}+101q^{97}-83q^{95}-254q^{93}-264q^{91}-56q^{89}+254q^{87}+430q^{85}+302q^{83}-97q^{81}-509q^{79}-598q^{77}-222q^{75}+401q^{73}+807q^{71}+646q^{69}-47q^{67}-815q^{65}-1046q^{63}-472q^{61}+536q^{59}+1230q^{57}+1048q^{55}+18q^{53}-1134q^{51}-1478q^{49}-684q^{47}+689q^{45}+1620q^{43}+1335q^{41}-39q^{39}-1442q^{37}-1752q^{35}-690q^{33}+971q^{31}+1897q^{29}+1304q^{27}-353q^{25}-1742q^{23}-1715q^{21}-259q^{19}+1399q^{17}+1862q^{15}+756q^{13}-964q^{11}-1823q^{9}-1061q^{7}+596q^{5}+1638q^{3}+1185q-312q^{-1}-1455q^{-3}-1182q^{-5}+185q^{-7}+1311q^{-9}+1128q^{-11}-141q^{-13}-1248q^{-15}-1124q^{-17}+117q^{-19}+1264q^{-21}+1196q^{-23}-30q^{-25}-1249q^{-27}-1354q^{-29}-222q^{-31}+1149q^{-33}+1534q^{-35}+617q^{-37}-825q^{-39}-1622q^{-41}-1134q^{-43}+275q^{-45}+1513q^{-47}+1612q^{-49}+475q^{-51}-1123q^{-53}-1936q^{-55}-1249q^{-57}+469q^{-59}+1937q^{-61}+1926q^{-63}+302q^{-65}-1639q^{-67}-2272q^{-69}-1034q^{-71}+1073q^{-73}+2285q^{-75}+1547q^{-77}-464q^{-79}-1967q^{-81}-1729q^{-83}-82q^{-85}+1471q^{-87}+1629q^{-89}+416q^{-91}-965q^{-93}-1316q^{-95}-521q^{-97}+538q^{-99}+936q^{-101}+481q^{-103}-265q^{-105}-602q^{-107}-339q^{-109}+118q^{-111}+335q^{-113}+209q^{-115}-50q^{-117}-176q^{-119}-107q^{-121}+33q^{-123}+87q^{-125}+35q^{-127}-19q^{-129}-37q^{-131}-15q^{-133}+15q^{-135}+19q^{-137}+q^{-139}-12q^{-141}-4q^{-143}+3q^{-145}+q^{-147}+q^{-149}+2q^{-151}-3q^{-153}-q^{-155}+4q^{-157}-2q^{-159}-q^{-161}+2q^{-163}-q^{-165}$

A2 Invariants.

Weight	Invariant
1,0	$-q^{12}-q^{8}-q^{6}+2q^{4}+3+2q^{-2}+2q^{-6}-2q^{-8}+q^{-10}-q^{-12}-q^{-14}+q^{-16}-q^{-18}$
1,1	$q^{36}-2q^{34}+8q^{32}-18q^{30}+35q^{28}-66q^{26}+104q^{24}-148q^{22}+190q^{20}-230q^{18}+248q^{16}-238q^{14}+201q^{12}-142q^{10}+52q^{8}+58q^{6}-163q^{4}+266q^{2}-354+420q^{-2}-440q^{-4}+432q^{-6}-382q^{-8}+316q^{-10}-213q^{-12}+118q^{-14}-24q^{-16}-60q^{-18}+115q^{-20}-154q^{-22}+168q^{-24}-178q^{-26}+166q^{-28}-146q^{-30}+126q^{-32}-110q^{-34}+87q^{-36}-62q^{-38}+48q^{-40}-36q^{-42}+22q^{-44}-12q^{-46}+8q^{-48}-4q^{-50}+q^{-52}$
2,0	$q^{34}-q^{30}+2q^{26}-4q^{22}-2q^{20}+4q^{18}-6q^{14}-q^{12}+4q^{10}+q^{8}-6q^{6}+2q^{4}+7q^{2}+6q^{-4}+q^{-6}-2q^{-8}+4q^{-10}+4q^{-12}-3q^{-14}-q^{-16}+7q^{-18}-10q^{-22}+4q^{-26}-5q^{-28}-5q^{-30}+2q^{-32}+3q^{-34}-q^{-36}-q^{-38}+2q^{-40}-q^{-44}+q^{-46}$

A3 Invariants.

Weight	Invariant
0,1,0	$q^{26}-q^{24}+2q^{22}+q^{20}-4q^{18}+3q^{16}-3q^{14}-10q^{12}+4q^{10}-3q^{8}-8q^{6}+13q^{4}+4q^{2}-2+14q^{-2}+6q^{-4}-5q^{-6}+2q^{-8}+2q^{-10}-q^{-12}-8q^{-14}+q^{-16}+6q^{-18}-11q^{-20}+10q^{-24}-10q^{-26}-2q^{-28}+10q^{-30}-6q^{-32}-3q^{-34}+6q^{-36}-q^{-38}-2q^{-40}+q^{-42}$
1,0,0	$-q^{15}-2q^{11}-2q^{7}+2q^{5}+4q+2q^{-1}+3q^{-3}+q^{-5}+q^{-9}-2q^{-11}+q^{-13}-2q^{-15}+q^{-17}-2q^{-19}+q^{-21}-q^{-23}$

A4 Invariants.

Weight	Invariant
0,1,0,0	$q^{32}+q^{28}+3q^{26}+q^{24}-q^{22}+2q^{20}-3q^{18}-10q^{16}-7q^{14}-6q^{12}-11q^{10}-10q^{8}+7q^{6}+11q^{4}+3q^{2}+13+26q^{-2}+10q^{-4}-q^{-6}+9q^{-8}+4q^{-10}-10q^{-12}-7q^{-14}+q^{-16}-5q^{-18}-11q^{-20}+3q^{-22}+3q^{-24}-9q^{-26}-2q^{-28}+8q^{-30}-2q^{-32}-7q^{-34}+3q^{-36}+5q^{-38}-2q^{-40}-4q^{-42}+3q^{-44}+3q^{-46}-2q^{-48}-q^{-50}+q^{-52}$
1,0,0,0	$-q^{18}-2q^{14}-q^{12}-q^{10}-2q^{8}+2q^{6}+4q^{2}+3+3q^{-2}+3q^{-4}+q^{-6}+q^{-8}-q^{-10}+q^{-12}-2q^{-14}+q^{-16}-2q^{-18}-2q^{-24}+q^{-26}-q^{-28}$

B2 Invariants.

Weight

Invariant

0,1

-q^{26}+q^{24}-4q^{22}+5q^{20}-8q^{18}+11q^{16}-13q^{14}+14q^{12}-14q^{10}+13q^{8}-8q^{6}+5q^{4}+4q^{2}-10+18q^{-2}-22q^{-4}+27q^{-6}-28q^{-8}+28q^{-10}-23q^{-12}+18q^{-14}-11q^{-16}+4q^{-18}+3q^{-20}-8q^{-22}+12q^{-24}-14q^{-26}+14q^{-28}-14q^{-30}+10q^{-32}-9q^{-34}+6q^{-36}-3q^{-38}+2q^{-40}-q^{-42}

1,0

q^{44}-q^{40}-q^{38}+3q^{36}+3q^{34}-3q^{32}-6q^{30}+8q^{26}+3q^{24}-11q^{22}-11q^{20}+4q^{18}+13q^{16}+q^{14}-16q^{12}-8q^{10}+11q^{8}+16q^{6}-2q^{4}-12q^{2}+14q^{-2}+8q^{-4}-5q^{-6}-5q^{-8}+7q^{-10}+7q^{-12}-5q^{-14}-9q^{-16}+4q^{-18}+10q^{-20}-2q^{-22}-13q^{-24}-4q^{-26}+11q^{-28}+7q^{-30}-10q^{-32}-12q^{-34}+4q^{-36}+14q^{-38}+2q^{-40}-12q^{-42}-9q^{-44}+6q^{-46}+12q^{-48}-8q^{-52}-6q^{-54}+3q^{-56}+6q^{-58}+q^{-60}-2q^{-62}-2q^{-64}+q^{-68}

D4 Invariants.

Weight

Invariant

1,0,0,0

q^{34}-q^{32}+3q^{30}-3q^{28}+6q^{26}-7q^{24}+7q^{22}-12q^{20}+8q^{18}-16q^{16}+6q^{14}-14q^{12}+8q^{10}-7q^{8}+5q^{6}+5q^{4}+4q^{2}+16-6q^{-2}+21q^{-4}-14q^{-6}+22q^{-8}-22q^{-10}+21q^{-12}-22q^{-14}+17q^{-16}-18q^{-18}+11q^{-20}-9q^{-22}+4q^{-24}-2q^{-26}-5q^{-28}+5q^{-30}-8q^{-32}+10q^{-34}-12q^{-36}+9q^{-38}-10q^{-40}+12q^{-42}-8q^{-44}+5q^{-46}-6q^{-48}+6q^{-50}-2q^{-52}+q^{-54}-2q^{-56}+q^{-58}

G2 Invariants.

Weight

Invariant

1,0

q^{60}-q^{58}+4q^{56}-6q^{54}+6q^{52}-6q^{50}-q^{48}+12q^{46}-25q^{44}+33q^{42}-31q^{40}+12q^{38}+14q^{36}-46q^{34}+64q^{32}-64q^{30}+38q^{28}-46q^{24}+71q^{22}-71q^{20}+46q^{18}-4q^{16}-32q^{14}+53q^{12}-47q^{10}+21q^{8}+18q^{6}-42q^{4}+56q^{2}-36+2q^{-2}+45q^{-4}-75q^{-6}+88q^{-8}-62q^{-10}+17q^{-12}+40q^{-14}-83q^{-16}+100q^{-18}-82q^{-20}+39q^{-22}+15q^{-24}-58q^{-26}+72q^{-28}-57q^{-30}+21q^{-32}+17q^{-34}-41q^{-36}+39q^{-38}-19q^{-40}-13q^{-42}+38q^{-44}-48q^{-46}+40q^{-48}-15q^{-50}-17q^{-52}+41q^{-54}-55q^{-56}+50q^{-58}-32q^{-60}+8q^{-62}+15q^{-64}-33q^{-66}+39q^{-68}-36q^{-70}+26q^{-72}-9q^{-74}-5q^{-76}+12q^{-78}-18q^{-80}+16q^{-82}-12q^{-84}+8q^{-86}-q^{-88}-2q^{-90}+3q^{-92}-4q^{-94}+3q^{-96}-2q^{-98}+q^{-100}

.

Computer Talk

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:= AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625.

In[3]:= K = Knot["10 52"];

In[4]:= Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]= $2t^{3}-7t^{2}+13t-15+13t^{-1}-7t^{-2}+2t^{-3}$

In[5]:= Conway[K][z]

Out[5]= $2z^{6}+5z^{4}+3z^{2}+1$

In[6]:= Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]= $\{1\}$

In[7]:= {KnotDet[K], KnotSignature[K]}

Out[7]= { 59, 2 }

In[8]:= Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]= $-q^{6}+3q^{5}-6q^{4}+8q^{3}-9q^{2}+10q-8+7q^{-1}-4q^{-2}+2q^{-3}-q^{-4}$

In[9]:= HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]= $z^{6}a^{-2}+z^{6}-a^{2}z^{4}+3z^{4}a^{-2}-z^{4}a^{-4}+4z^{4}-3a^{2}z^{2}+2z^{2}a^{-2}-2z^{2}a^{-4}+6z^{2}-2a^{2}-a^{-4}+4$

In[10]:= Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]= $az^{9}+z^{9}a^{-1}+2a^{2}z^{8}+4z^{8}a^{-2}+6z^{8}+a^{3}z^{7}+az^{7}+7z^{7}a^{-1}+7z^{7}a^{-3}-9a^{2}z^{6}-3z^{6}a^{-2}+8z^{6}a^{-4}-20z^{6}-5a^{3}z^{5}-16az^{5}-28z^{5}a^{-1}-11z^{5}a^{-3}+6z^{5}a^{-5}+13a^{2}z^{4}-9z^{4}a^{-2}-12z^{4}a^{-4}+3z^{4}a^{-6}+19z^{4}+8a^{3}z^{3}+24az^{3}+24z^{3}a^{-1}+2z^{3}a^{-3}-5z^{3}a^{-5}+z^{3}a^{-7}-7a^{2}z^{2}+4z^{2}a^{-2}+6z^{2}a^{-4}-9z^{2}-4a^{3}z-9az-7za^{-1}+2za^{-5}+2a^{2}-a^{-4}+4$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {10_23,}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$ ): {}

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:= AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091.

In[3]:= K = Knot["10 52"];

In[4]:= {A = Alexander[K][t], J = Jones[K][q]}

KnotTheory::loading: Loading precomputed data in PD4Knots`.

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[4]= { $2t^{3}-7t^{2}+13t-15+13t^{-1}-7t^{-2}+2t^{-3}$ , $-q^{6}+3q^{5}-6q^{4}+8q^{3}-9q^{2}+10q-8+7q^{-1}-4q^{-2}+2q^{-3}-q^{-4}$ }

In[5]:= DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]

KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.

KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

Out[5]= {10_23,}

In[6]:= DeleteCases[ Select[ AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) & ], K ]

KnotTheory::loading: Loading precomputed data in Jones4Knots11`.

Out[6]= {}

Vassiliev invariants

V₂ and V₃:

(3, 1)

V_2,1 through V_6,9:

V_2,1

V_3,1

V_4,1

V_4,2

V_4,3

V_5,1

V_5,2

V_5,3

V_5,4

V_6,1

V_6,2

V_6,3

V_6,4

V_6,5

V_6,6

V_6,7

V_6,8

V_6,9

12

8

72

78

-6

96

{\frac {464}{3}}

-{\frac {64}{3}}

72

288

32

936

-72

{\frac {10591}{10}}

{\frac {778}{5}}

{\frac {1462}{15}}

{\frac {289}{6}}

-{\frac {769}{10}}

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials

t^{r}q^{j}

are shown, along with their alternating sums

\chi

(fixed

j

, alternation over

r

). The squares with yellow highlighting are those on the "critical diagonals", where

j-2r=s+1

or

j-2r=s-1

, where

s=

2 is the signature of 10 52. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\		r
	\
j		\

-5

-4

-3

-2

-1

0

1

2

3

4

5

χ

13

1

-1

11

2

9

4

1

-3

7

4

2

5

4

-1

3

5

4

1

4

6

2

-1

3

4

-1

-3

1

4

3

-5

1

3

-2

-7

1

-9

1

-1

Integral Khovanov Homology

(db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$	$i=1$	$i=3$
$r=-5$	${\mathbb {Z} }$
$r=-4$	${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$	${\mathbb {Z} }$
$r=-3$	${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}$	${\mathbb {Z} }$
$r=-2$	${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{3}$	${\mathbb {Z} }^{3}$
$r=-1$	${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{4}$	${\mathbb {Z} }^{4}$
$r=0$	${\mathbb {Z} }^{6}\oplus {\mathbb {Z} }_{2}^{4}$	${\mathbb {Z} }^{5}$
$r=1$	${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{5}$	${\mathbb {Z} }^{5}$
$r=2$	${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{4}$	${\mathbb {Z} }^{4}$
$r=3$	${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}^{4}$	${\mathbb {Z} }^{4}$
$r=4$	${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{2}$	${\mathbb {Z} }^{2}$
$r=5$	${\mathbb {Z} }_{2}$	${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the

n+1

-dimensional representation of

sl(2)

)

$n$	$J_{n}$
2	$q^{17}-3q^{16}+3q^{15}+4q^{14}-15q^{13}+14q^{12}+9q^{11}-37q^{10}+31q^{9}+17q^{8}-60q^{7}+41q^{6}+30q^{5}-73q^{4}+35q^{3}+43q^{2}-70q+20+46q^{-1}-52q^{-2}+3q^{-3}+37q^{-4}-28q^{-5}-6q^{-6}+21q^{-7}-9q^{-8}-6q^{-9}+7q^{-10}-q^{-11}-2q^{-12}+q^{-13}$
3	$-q^{33}+3q^{32}-3q^{31}-q^{30}+3q^{29}+4q^{28}-9q^{27}-4q^{26}+19q^{25}+2q^{24}-35q^{23}+5q^{22}+53q^{21}-9q^{20}-85q^{19}+20q^{18}+117q^{17}-22q^{16}-156q^{15}+18q^{14}+190q^{13}-6q^{12}-210q^{11}-24q^{10}+228q^{9}+47q^{8}-216q^{7}-88q^{6}+211q^{5}+107q^{4}-173q^{3}-145q^{2}+155q+150-108q^{-1}-169q^{-2}+80q^{-3}+160q^{-4}-35q^{-5}-155q^{-6}+6q^{-7}+130q^{-8}+26q^{-9}-105q^{-10}-43q^{-11}+73q^{-12}+49q^{-13}-41q^{-14}-48q^{-15}+20q^{-16}+34q^{-17}-2q^{-18}-24q^{-19}-2q^{-20}+11q^{-21}+5q^{-22}-6q^{-23}-2q^{-24}+q^{-25}+2q^{-26}-q^{-27}$
4	$q^{54}-3q^{53}+3q^{52}+q^{51}-6q^{50}+8q^{49}-9q^{48}+10q^{47}-2q^{46}-22q^{45}+36q^{44}-19q^{43}+15q^{42}-20q^{41}-51q^{40}+111q^{39}-21q^{38}-8q^{37}-91q^{36}-82q^{35}+286q^{34}+19q^{33}-92q^{32}-277q^{31}-149q^{30}+581q^{29}+185q^{28}-178q^{27}-595q^{26}-343q^{25}+880q^{24}+481q^{23}-120q^{22}-888q^{21}-673q^{20}+978q^{19}+743q^{18}+122q^{17}-958q^{16}-977q^{15}+825q^{14}+792q^{13}+416q^{12}-776q^{11}-1114q^{10}+543q^{9}+643q^{8}+630q^{7}-478q^{6}-1085q^{5}+249q^{4}+407q^{3}+749q^{2}-163q-955-23q^{-1}+149q^{-2}+778q^{-3}+137q^{-4}-728q^{-5}-233q^{-6}-134q^{-7}+672q^{-8}+375q^{-9}-396q^{-10}-294q^{-11}-378q^{-12}+404q^{-13}+442q^{-14}-49q^{-15}-163q^{-16}-454q^{-17}+88q^{-18}+300q^{-19}+141q^{-20}+39q^{-21}-321q^{-22}-88q^{-23}+84q^{-24}+123q^{-25}+134q^{-26}-125q^{-27}-83q^{-28}-30q^{-29}+31q^{-30}+97q^{-31}-17q^{-32}-23q^{-33}-32q^{-34}-11q^{-35}+35q^{-36}+3q^{-37}+2q^{-38}-9q^{-39}-9q^{-40}+7q^{-41}+q^{-42}+2q^{-43}-q^{-44}-2q^{-45}+q^{-46}$
5	$-q^{80}+3q^{79}-3q^{78}-q^{77}+6q^{76}-5q^{75}-3q^{74}+8q^{73}-4q^{72}-q^{71}+8q^{70}-12q^{69}-11q^{68}+21q^{67}+14q^{66}-5q^{65}-22q^{64}-34q^{63}+7q^{62}+75q^{61}+66q^{60}-59q^{59}-162q^{58}-103q^{57}+133q^{56}+334q^{55}+192q^{54}-276q^{53}-619q^{52}-366q^{51}+470q^{50}+1080q^{49}+647q^{48}-674q^{47}-1678q^{46}-1161q^{45}+821q^{44}+2461q^{43}+1860q^{42}-832q^{41}-3231q^{40}-2808q^{39}+583q^{38}+3964q^{37}+3871q^{36}-94q^{35}-4443q^{34}-4915q^{33}-655q^{32}+4597q^{31}+5812q^{30}+1530q^{29}-4432q^{28}-6383q^{27}-2373q^{26}+3910q^{25}+6625q^{24}+3128q^{23}-3295q^{22}-6482q^{21}-3611q^{20}+2501q^{19}+6137q^{18}+3925q^{17}-1853q^{16}-5565q^{15}-3996q^{14}+1130q^{13}+5005q^{12}+4030q^{11}-634q^{10}-4339q^{9}-3928q^{8}-17q^{7}+3764q^{6}+3906q^{5}+473q^{4}-3070q^{3}-3745q^{2}-1143q+2397+3633q^{-1}+1616q^{-2}-1573q^{-3}-3292q^{-4}-2185q^{-5}+740q^{-6}+2871q^{-7}+2475q^{-8}+147q^{-9}-2186q^{-10}-2648q^{-11}-918q^{-12}+1415q^{-13}+2448q^{-14}+1536q^{-15}-529q^{-16}-2055q^{-17}-1844q^{-18}-246q^{-19}+1386q^{-20}+1846q^{-21}+874q^{-22}-681q^{-23}-1559q^{-24}-1177q^{-25}+13q^{-26}+1052q^{-27}+1218q^{-28}+471q^{-29}-529q^{-30}-995q^{-31}-681q^{-32}+44q^{-33}+644q^{-34}+702q^{-35}+239q^{-36}-302q^{-37}-520q^{-38}-362q^{-39}+21q^{-40}+326q^{-41}+328q^{-42}+110q^{-43}-121q^{-44}-234q^{-45}-155q^{-46}+16q^{-47}+120q^{-48}+120q^{-49}+50q^{-50}-50q^{-51}-81q^{-52}-39q^{-53}+2q^{-54}+32q^{-55}+40q^{-56}+8q^{-57}-19q^{-58}-13q^{-59}-8q^{-60}-2q^{-61}+11q^{-62}+7q^{-63}-3q^{-64}-2q^{-65}-q^{-66}-2q^{-67}+q^{-68}+2q^{-69}-q^{-70}$
6	$q^{111}-3q^{110}+3q^{109}+q^{108}-6q^{107}+5q^{106}+4q^{104}-14q^{103}+7q^{102}+15q^{101}-26q^{100}+18q^{99}+5q^{98}-5q^{97}-37q^{96}+22q^{95}+59q^{94}-62q^{93}+23q^{92}-6q^{91}-42q^{90}-55q^{89}+123q^{88}+192q^{87}-164q^{86}-100q^{85}-170q^{84}-129q^{83}+115q^{82}+596q^{81}+612q^{80}-468q^{79}-798q^{78}-963q^{77}-422q^{76}+901q^{75}+2241q^{74}+1962q^{73}-996q^{72}-2896q^{71}-3549q^{70}-1659q^{69}+2553q^{68}+6269q^{67}+5743q^{66}-877q^{65}-6779q^{64}-9469q^{63}-5700q^{62}+3925q^{61}+12961q^{60}+13693q^{59}+2283q^{58}-10692q^{57}-18675q^{56}-14467q^{55}+1913q^{54}+19644q^{53}+25210q^{52}+10645q^{51}-10654q^{50}-27467q^{49}-26739q^{48}-5805q^{47}+21506q^{46}+35577q^{45}+22409q^{44}-4323q^{43}-30514q^{42}-37060q^{41}-16824q^{40}+16488q^{39}+39319q^{38}+31754q^{37}+5350q^{36}-26325q^{35}-40357q^{34}-25325q^{33}+8043q^{32}+35758q^{31}+34436q^{30}+12861q^{29}-18752q^{28}-36938q^{27}-28088q^{26}+1142q^{25}+29006q^{24}+31710q^{23}+16027q^{22}-12149q^{21}-31018q^{20}-27007q^{19}-2896q^{18}+22750q^{17}+27575q^{16}+16999q^{15}-7174q^{14}-25518q^{13}-25488q^{12}-6194q^{11}+17092q^{10}+24019q^{9}+18392q^{8}-1873q^{7}-19974q^{6}-24460q^{5}-10547q^{4}+10191q^{3}+19883q^{2}+20150q+4894-12517q^{-1}-22066q^{-2}-15065q^{-3}+1389q^{-4}+13095q^{-5}+19786q^{-6}+11592q^{-7}-2785q^{-8}-16031q^{-9}-16720q^{-10}-7209q^{-11}+3498q^{-12}+14845q^{-13}+14724q^{-14}+6619q^{-15}-6482q^{-16}-12944q^{-17}-11647q^{-18}-5804q^{-19}+5821q^{-20}+11713q^{-21}+11350q^{-22}+2872q^{-23}-4696q^{-24}-9434q^{-25}-10155q^{-26}-2946q^{-27}+4098q^{-28}+9167q^{-29}+7129q^{-30}+3105q^{-31}-2746q^{-32}-7734q^{-33}-6493q^{-34}-2737q^{-35}+2923q^{-36}+4996q^{-37}+5710q^{-38}+2795q^{-39}-2027q^{-40}-4233q^{-41}-4522q^{-42}-1751q^{-43}+410q^{-44}+3331q^{-45}+3671q^{-46}+1653q^{-47}-388q^{-48}-2254q^{-49}-2234q^{-50}-1967q^{-51}+205q^{-52}+1545q^{-53}+1705q^{-54}+1224q^{-55}+85q^{-56}-615q^{-57}-1500q^{-58}-825q^{-59}-141q^{-60}+428q^{-61}+743q^{-62}+616q^{-63}+362q^{-64}-403q^{-65}-411q^{-66}-382q^{-67}-170q^{-68}+64q^{-69}+249q^{-70}+340q^{-71}+25q^{-72}-16q^{-73}-124q^{-74}-126q^{-75}-99q^{-76}+6q^{-77}+115q^{-78}+30q^{-79}+45q^{-80}-q^{-81}-20q^{-82}-48q^{-83}-23q^{-84}+23q^{-85}+15q^{-87}+7q^{-88}+5q^{-89}-11q^{-90}-9q^{-91}+5q^{-92}-2q^{-93}+2q^{-94}+q^{-95}+2q^{-96}-q^{-97}-2q^{-98}+q^{-99}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session, or any of the Computer Talk sections above.

Modifying This Page

Read me first: Modifying Knot Pages

See/edit the Rolfsen Knot Page master template (intermediate).

See/edit the Rolfsen_Splice_Base (expert).

Back to the top.

10_51

10_53

10 52

Contents

Knot presentations

Three dimensional invariants

Four dimensional invariants

Polynomial invariants

"Similar" Knots (within the Atlas)

Vassiliev invariants

Khovanov Homology

The Coloured Jones Polynomials

Computer Talk

Modifying This Page

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

Tools