L2a1
From Knot Atlas
Jump to navigationJump to search
|
|
|

|
Visit L2a1's page at Knotilus!
Visit L2a1's page at the original Knot Atlas! |
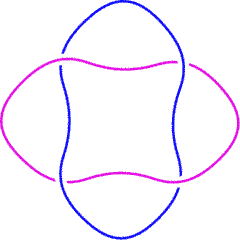
| L2a1 is [math]\displaystyle{ 2^2_1 }[/math] in Rolfsen's table of links. It is also known as the "Hopf Link".
The sheet bend of practical knot tying deforms to the Hopf link. |
 expanded Kolam Two-hearts [1] |
|||
 Are they forever linked? [2] |
Knot presentations
| Planar diagram presentation | X4132 X2314 |
| Gauss code | {1, -2}, {2, -1} |
Polynomial invariants
| Multivariable Alexander Polynomial (in [math]\displaystyle{ u }[/math], [math]\displaystyle{ v }[/math], [math]\displaystyle{ w }[/math], ...) | [math]\displaystyle{ -1 }[/math] (db) |
| Jones polynomial | [math]\displaystyle{ -\frac{1}{\sqrt{q}}-\frac{1}{q^{5/2}} }[/math] (db) |
| Signature | -1 (db) |
| HOMFLY-PT polynomial | [math]\displaystyle{ a^3 z^{-1} -z a-a z^{-1} }[/math] (db) |
| Kauffman polynomial | [math]\displaystyle{ -z a^3+a^3 z^{-1} -a^2-z a+a z^{-1} }[/math] (db) |
Vassiliev invariants
| V2 and V3: | (0, [math]\displaystyle{ -\frac{17}{48} }[/math]) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
| The coefficients of the monomials [math]\displaystyle{ t^rq^j }[/math] are shown, along with their alternating sums [math]\displaystyle{ \chi }[/math] (fixed [math]\displaystyle{ j }[/math], alternation over [math]\displaystyle{ r }[/math]). The squares with yellow highlighting are those on the "critical diagonals", where [math]\displaystyle{ j-2r=s+1 }[/math] or [math]\displaystyle{ j-2r=s-1 }[/math], where [math]\displaystyle{ s= }[/math]-1 is the signature of L2a1. Nonzero entries off the critical diagonals (if any exist) are highlighted in red. |
|
| Integral Khovanov Homology
(db, data source) |
|
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
[math]\displaystyle{ \textrm{Include}(\textrm{ColouredJonesM.mhtml}) }[/math]
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 17, 2005, 14:44:34)... | |
In[2]:= | Crossings[Link[2, Alternating, 1]] |
Out[2]= | 2 |
In[3]:= | PD[Link[2, Alternating, 1]] |
Out[3]= | PD[X[4, 1, 3, 2], X[2, 3, 1, 4]] |
In[4]:= | GaussCode[Link[2, Alternating, 1]] |
Out[4]= | GaussCode[{1, -2}, {2, -1}] |
In[5]:= | BR[Link[2, Alternating, 1]] |
Out[5]= | BR[Link[2, Alternating, 1]] |
In[6]:= | alex = Alexander[Link[2, Alternating, 1]][t] |
Out[6]= | ComplexInfinity |
In[7]:= | Conway[Link[2, Alternating, 1]][z] |
Out[7]= | ComplexInfinity |
In[8]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[8]= | {} |
In[9]:= | {KnotDet[Link[2, Alternating, 1]], KnotSignature[Link[2, Alternating, 1]]} |
Out[9]= | {Infinity, -1} |
In[10]:= | J=Jones[Link[2, Alternating, 1]][q] |
Out[10]= | -(5/2) 1 |
In[11]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[11]= | {} |
In[12]:= | A2Invariant[Link[2, Alternating, 1]][q] |
Out[12]= | -10 2 2 2 -2 |
In[13]:= | Kauffman[Link[2, Alternating, 1]][a, z] |
Out[13]= | 32 a a 3 |
In[14]:= | {Vassiliev[2][Link[2, Alternating, 1]], Vassiliev[3][Link[2, Alternating, 1]]} |
Out[14]= | 17 |
In[15]:= | Kh[Link[2, Alternating, 1]][q, t] |
Out[15]= | -2 1 1 |