Finite Type (Vassiliev) Invariants
From Knot Atlas
Jump to navigationJump to search
(For In[1] see Setup)
In[1]:= ?Vassiliev
Vassiliev[2][K] computes the (standardly normalized) type 2 Vassiliev invariant of the knot K, i.e., the coefficient of z^2 in Conway[K][z]. Vassiliev[3][K] computes the (standardly normalized) type 3 Vassiliev invariant of the knot K, i.e., 3J(1)-(1/36)J'(1) where J is the Jones polynomial of K. |
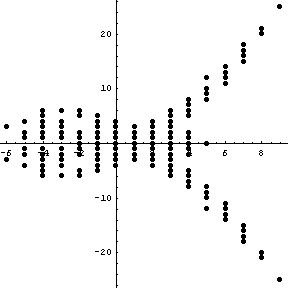
Thus, for example, let us reproduce Willerton's "fish" (arXiv:math.GT/0104061), the result of plotting the values of against the values of , where is the (standardly normalized) type 2 invariant of , is the (standardly normalized) type 3 invariant of , and where runs over a set of knots with equal crossing numbers (10, in the example below):