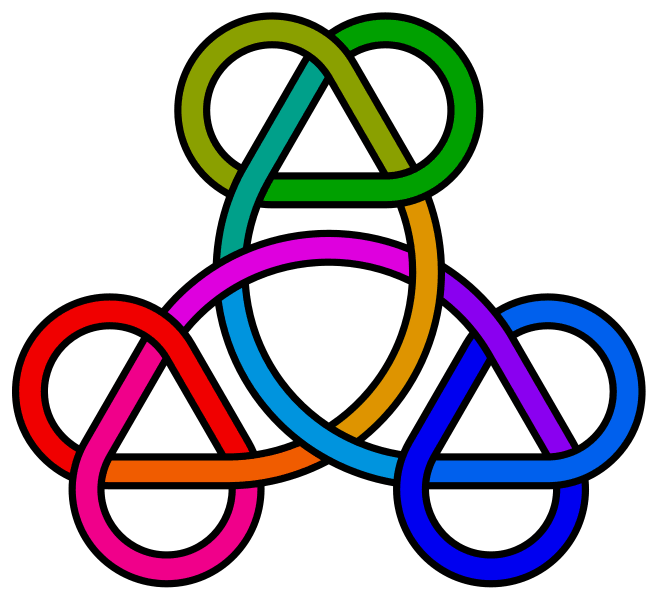3 1

{{Rolfsen Knot Page]], which actually produces this page. {{Rolfsen Knot Page]] setting the values of all the parameters appropriately.

0_1

4_1

(KnotPlot image)	See the full Rolfsen Knot Table. Visit 3 1's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 3 1 at Knotilus!
	3_1 is also known as "The Trefoil Knot", after plants of the genus Trifolium, which have compound trifoliate leaves, and as the "Overhand Knot". See also T(3,2).

The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:

Logo of Caixa Geral de Depositos, Lisboa [1]

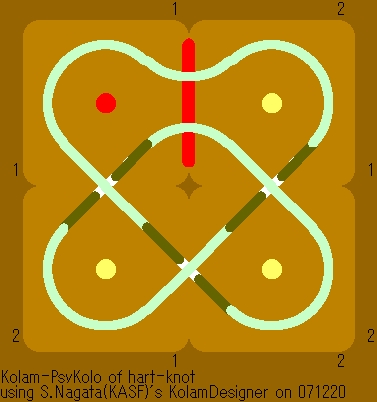A knot consists of two harts in Kolam [2]

A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity

3D depiction

Further images...[show]

Trefoil/triquetra without outside corners (made from straight lines and 240° circular arcs)	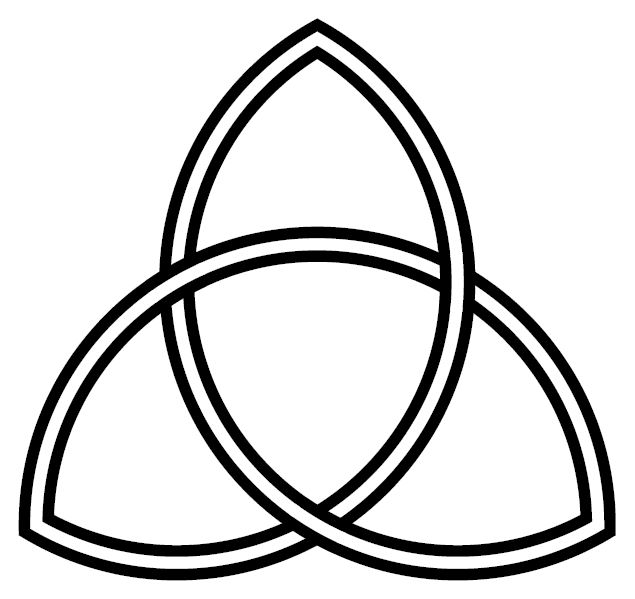Triquetra made from circular arc ribbons	Tightly-knotted form	Celtic-style
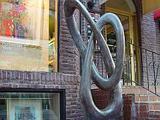A Knotted Box [3]	A trefoil near the Hollander York Gallery [4]	Trefoil of three intersecting circles	Trefoil depicted in non-threefold form
3D depiction in non-threefold form	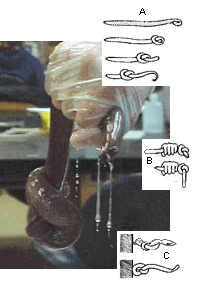A hagfish tying itself in a knot to escape capture. [5]	One version of the Germanic "Valknut" symbol	A Kenyan Stone [6]
Square depiction	In the form of an architectural trefoil	Polar equation curve.	Alternate Valknut depiction
Simple overhand knot of practical knot-tying	Tightly folded pentagonal overhand knot	Visually fancier square trefoil	Trefoil knot as impossible object
Logo of the Caixa Geral de Depósitos with white background	The NeverEnding Story logo is a connected sum of two trefoils. [7]	Mike Hutchings' Rope Trick [8]	Thurston's Trefoil - Figure Eight Trick [9]
A Knotted Pencil [10]	Banco Do Brasil [11]

Non-prime (compound) versions

• 

  Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

• 

  Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

• 

  3D square knot

• 

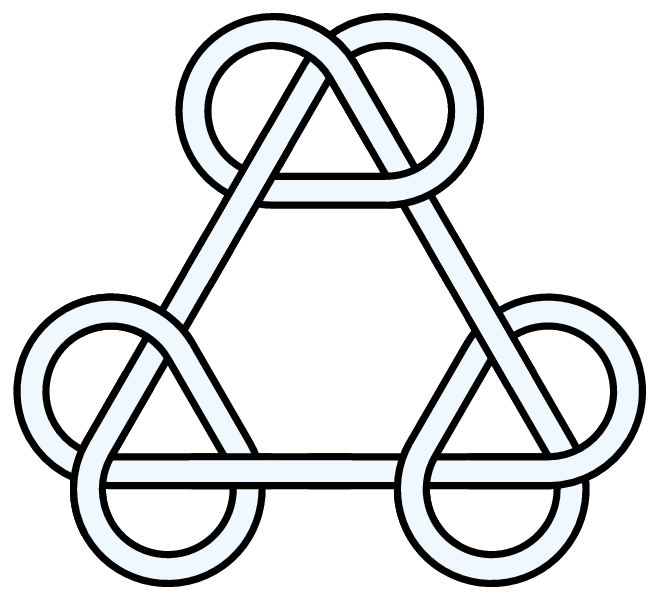
  Three trefoils (symmetrical).

• 

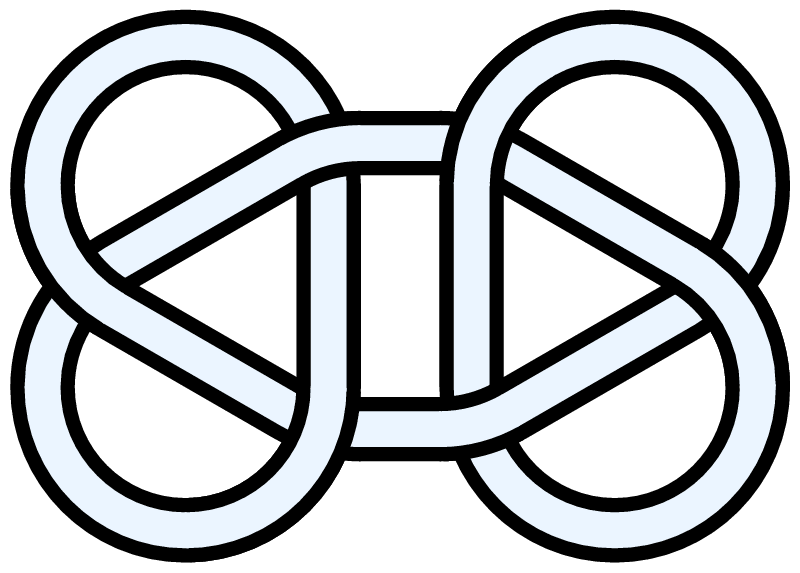
  Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

• 

  Three trefoils along a closed loop which itself is knotted as a trefoil.

• 

  Sum of four trefoils, Multan, Pakistan

For configurations of two trefoils along a closed loop which are prime, see 8_15 and 10_120. For a configuration of three trefoils along a closed loop which is prime, see K13a248. For a prime link consisting of two joined trefoils, see L10a108.

Knot presentations

Planar diagram presentation	X1425 X3641 X5263
Gauss code	-1, 3, -2, 1, -3, 2
Dowker-Thistlethwaite code	4 6 2
Conway Notation	[3]

Minimum Braid Representative	A Morse Link Presentation	An Arc Presentation
Length is 3, width is 2, Braid index is 2		[{5, 2}, {1, 3}, {2, 4}, {3, 5}, {4, 1}]

[edit Notes on presentations of 3 1]

Knot 3_1.

A graph, knot 3_1.

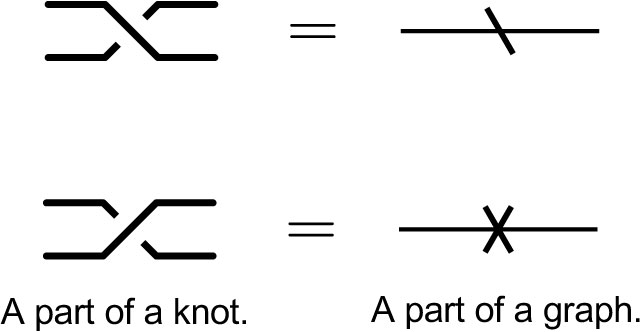A part of a knot and a part of a graph.

Computer Talk[show]

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.org/wiki/KnotTheory.

In[3]:=

K = Knot["3 1"];

In[4]:=

PD[K]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

X1425 X3641 X5263

In[5]:=

GaussCode[K]

Out[5]=

-1, 3, -2, 1, -3, 2

In[6]:=

DTCode[K]

Out[6]=

4 6 2

(The path below may be different on your system)

In[7]:=

AppendTo[$Path, "C:/bin/LinKnot/"];

In[8]:=

ConwayNotation[K]

Out[8]=

[3]

In[9]:=

br = BR[K]

KnotTheory::credits: The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See arXiv:math.GT/0401051.

Out[9]=

${\textrm {BR}}(2,\{-1,-1,-1\})$

In[10]:=

{First[br], Crossings[br], BraidIndex[K]}

KnotTheory::credits: The braid index data known to KnotTheory` is taken from Charles Livingston's http://www.indiana.edu/~knotinfo/.

KnotTheory::loading: Loading precomputed data in IndianaData`.

Out[10]=

{ 2, 3, 2 }

In[11]:=

Show[BraidPlot[br]]

Out[11]=

-Graphics-

In[12]:=

Show[DrawMorseLink[K]]

KnotTheory::credits: "MorseLink was added to KnotTheory` by Siddarth Sankaran at the University of Toronto in the summer of 2005."

KnotTheory::credits: "DrawMorseLink was written by Siddarth Sankaran at the University of Toronto in the summer of 2005."

Out[12]=

-Graphics-

In[13]:=

ap = ArcPresentation[K]

Out[13]=

ArcPresentation[{5, 2}, {1, 3}, {2, 4}, {3, 5}, {4, 1}]

In[14]:=

Draw[ap]

Out[14]=

-Graphics-

Three dimensional invariants

Symmetry type Reversible Unknotting number 1 3-genus 1 Bridge index 2 Super bridge index 3 Nakanishi index 1 Maximal Thurston-Bennequin number [-6][1] Hyperbolic Volume Not hyperbolic A-Polynomial See Data:3 1/A-polynomial

[edit Notes for 3 1's three dimensional invariants] The rope length of the trefoil is known to be no more than 16.372, by numerical experiments, while the sharpest known lower bound (actually applicable to all non-trivial knots) is 15.66. The trefoil is a fibered knot! A java applet demonstrating it, written by Robert Barrington Leigh at the University of Toronto, is here.

Four dimensional invariants

Smooth 4 genus $1$ Topological 4 genus $1$ Concordance genus ${\textrm {ConcordanceGenus}}({\textrm {Knot}}(3,1))$ Rasmussen s-Invariant -2

[edit Notes for 3 1's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$t+t^{-1}-1$
Conway polynomial	$z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 3, -2 }
Jones polynomial	$-q^{-4}+q^{-3}+q^{-1}$
HOMFLY-PT polynomial (db, data sources)	$-a^{4}+a^{2}z^{2}+2a^{2}$
Kauffman polynomial (db, data sources)	$a^{5}z+a^{4}z^{2}-a^{4}+a^{3}z+a^{2}z^{2}-2a^{2}$
The A2 invariant	$-q^{14}-q^{12}+q^{8}+2q^{6}+q^{4}+q^{2}$
The G2 invariant	$q^{72}-q^{64}-q^{62}-q^{56}-2q^{54}-q^{52}+q^{50}-q^{46}-2q^{44}+2q^{40}+q^{38}-q^{36}+2q^{32}+2q^{30}+q^{28}+2q^{22}+2q^{20}+q^{14}+q^{12}+q^{10}$

Further Quantum Invariants[show]

Further quantum knot invariants for 3_1.

The braid index of 3_1 is only 2, so it's easy to calculate lots of quantum invariants. A1 Invariants.

Weight	Invariant
1	$-q^{9}+q^{5}+q^{3}+q$
2	$q^{24}-q^{20}-q^{18}-q^{16}+q^{10}+q^{8}+q^{6}+q^{4}+q^{2}$
3	$-q^{45}+q^{41}+q^{39}+q^{37}-q^{31}-q^{29}-q^{27}-q^{25}-q^{23}+q^{15}+q^{13}+q^{11}+q^{9}+q^{7}+q^{5}+q^{3}$
4	$q^{72}-q^{68}-q^{66}-q^{64}+q^{58}+q^{56}+q^{54}+q^{52}+q^{50}-q^{42}-q^{40}-q^{38}-q^{36}-q^{34}-q^{32}-q^{30}+q^{20}+q^{18}+q^{16}+q^{14}+q^{12}+q^{10}+q^{8}+q^{6}+q^{4}$
5	$-q^{105}+q^{101}+q^{99}+q^{97}-q^{91}-q^{89}-q^{87}-q^{85}-q^{83}+q^{75}+q^{73}+q^{71}+q^{69}+q^{67}+q^{65}+q^{63}-q^{53}-q^{51}-q^{49}-q^{47}-q^{45}-q^{43}-q^{41}-q^{39}-q^{37}+q^{25}+q^{23}+q^{21}+q^{19}+q^{17}+q^{15}+q^{13}+q^{11}+q^{9}+q^{7}+q^{5}$
6	$q^{144}-q^{140}-q^{138}-q^{136}+q^{130}+q^{128}+q^{126}+q^{124}+q^{122}-q^{114}-q^{112}-q^{110}-q^{108}-q^{106}-q^{104}-q^{102}+q^{92}+q^{90}+q^{88}+q^{86}+q^{84}+q^{82}+q^{80}+q^{78}+q^{76}-q^{64}-q^{62}-q^{60}-q^{58}-q^{56}-q^{54}-q^{52}-q^{50}-q^{48}-q^{46}-q^{44}+q^{30}+q^{28}+q^{26}+q^{24}+q^{22}+q^{20}+q^{18}+q^{16}+q^{14}+q^{12}+q^{10}+q^{8}+q^{6}$
8	$q^{240}-q^{236}-q^{234}-q^{232}+q^{226}+q^{224}+q^{222}+q^{220}+q^{218}-q^{210}-q^{208}-q^{206}-q^{204}-q^{202}-q^{200}-q^{198}+q^{188}+q^{186}+q^{184}+q^{182}+q^{180}+q^{178}+q^{176}+q^{174}+q^{172}-q^{160}-q^{158}-q^{156}-q^{154}-q^{152}-q^{150}-q^{148}-q^{146}-q^{144}-q^{142}-q^{140}+q^{126}+q^{124}+q^{122}+q^{120}+q^{118}+q^{116}+q^{114}+q^{112}+q^{110}+q^{108}+q^{106}+q^{104}+q^{102}-q^{86}-q^{84}-q^{82}-q^{80}-q^{78}-q^{76}-q^{74}-q^{72}-q^{70}-q^{68}-q^{66}-q^{64}-q^{62}-q^{60}-q^{58}+q^{40}+q^{38}+q^{36}+q^{34}+q^{32}+q^{30}+q^{28}+q^{26}+q^{24}+q^{22}+q^{20}+q^{18}+q^{16}+q^{14}+q^{12}+q^{10}+q^{8}$

A2 Invariants.

Weight	Invariant
0,1	$-q^{14}-q^{12}+q^{8}+2q^{6}+q^{4}+q^{2}$
0,2	$q^{34}+q^{32}+q^{30}-q^{28}-2q^{26}-3q^{24}-3q^{22}-q^{20}+2q^{16}+2q^{14}+3q^{12}+2q^{10}+2q^{8}+q^{6}+q^{4}$
1,0	$-q^{14}-q^{12}+q^{8}+2q^{6}+q^{4}+q^{2}$
1,1	$q^{36}-2q^{24}-2q^{22}-3q^{20}-2q^{18}+2q^{14}+3q^{12}+4q^{10}+4q^{8}+2q^{6}+q^{4}$
2,0	$q^{34}+q^{32}+q^{30}-q^{28}-2q^{26}-3q^{24}-3q^{22}-q^{20}+2q^{16}+2q^{14}+3q^{12}+2q^{10}+2q^{8}+q^{6}+q^{4}$
3,0	$-q^{60}-q^{58}-q^{56}+2q^{52}+3q^{50}+4q^{48}+3q^{46}+2q^{44}-q^{42}-3q^{40}-5q^{38}-5q^{36}-5q^{34}-4q^{32}-2q^{30}-q^{28}+q^{26}+2q^{24}+3q^{22}+3q^{20}+4q^{18}+3q^{16}+3q^{14}+2q^{12}+2q^{10}+q^{8}+q^{6}$

A3 Invariants.

Weight	Invariant
0,0,1	$-q^{19}-q^{17}-q^{15}+q^{11}+2q^{9}+2q^{7}+q^{5}+q^{3}$
0,1,0	$q^{30}-q^{24}-2q^{22}-2q^{20}-2q^{18}+q^{14}+3q^{12}+3q^{10}+3q^{8}+q^{6}+q^{4}$
1,0,0	$-q^{19}-q^{17}-q^{15}+q^{11}+2q^{9}+2q^{7}+q^{5}+q^{3}$
1,0,1	$q^{48}+q^{38}+q^{36}+q^{34}-q^{32}-3q^{30}-5q^{28}-6q^{26}-6q^{24}-3q^{22}+q^{20}+4q^{18}+7q^{16}+8q^{14}+7q^{12}+5q^{10}+2q^{8}+q^{6}$

A4 Invariants.

Weight	Invariant
0,0,0,1	$-q^{24}-q^{22}-q^{20}-q^{18}+q^{14}+2q^{12}+2q^{10}+2q^{8}+q^{6}+q^{4}$
0,1,0,0	$q^{40}+q^{38}+q^{36}-q^{32}-3q^{30}-4q^{28}-4q^{26}-3q^{24}-q^{22}+q^{20}+4q^{18}+4q^{16}+5q^{14}+4q^{12}+3q^{10}+q^{8}+q^{6}$
1,0,0,0	$-q^{24}-q^{22}-q^{20}-q^{18}+q^{14}+2q^{12}+2q^{10}+2q^{8}+q^{6}+q^{4}$

A5 Invariants.

Weight	Invariant
0,0,0,0,1	$-q^{29}-q^{27}-q^{25}-q^{23}-q^{21}+q^{17}+2q^{15}+2q^{13}+2q^{11}+2q^{9}+q^{7}+q^{5}$
1,0,0,0,0	$-q^{29}-q^{27}-q^{25}-q^{23}-q^{21}+q^{17}+2q^{15}+2q^{13}+2q^{11}+2q^{9}+q^{7}+q^{5}$

A6 Invariants.

Weight	Invariant
0,0,0,0,0,1	$-q^{34}-q^{32}-q^{30}-q^{28}-q^{26}-q^{24}+q^{20}+2q^{18}+2q^{16}+2q^{14}+2q^{12}+2q^{10}+q^{8}+q^{6}$
1,0,0,0,0,0	$-q^{34}-q^{32}-q^{30}-q^{28}-q^{26}-q^{24}+q^{20}+2q^{18}+2q^{16}+2q^{14}+2q^{12}+2q^{10}+q^{8}+q^{6}$

B2 Invariants.

Weight	Invariant
0,1	$-q^{30}-q^{24}+q^{14}+q^{12}+q^{10}+q^{8}+q^{6}+q^{4}$
1,0	$q^{48}-q^{38}-q^{36}-q^{34}-q^{32}-q^{30}-q^{28}+q^{22}+q^{20}+2q^{18}+q^{16}+2q^{14}+q^{12}+q^{10}+q^{6}$

B3 Invariants.

Weight	Invariant
1,0,0	$q^{72}-q^{58}-q^{54}-q^{52}-q^{50}-q^{48}-q^{46}-q^{44}-q^{42}+q^{34}+2q^{30}+q^{28}+2q^{26}+q^{24}+2q^{22}+q^{20}+2q^{18}+q^{14}+q^{10}$

B4 Invariants.

Weight	Invariant
1,0,0,0	$q^{96}-q^{78}-q^{74}-q^{70}-q^{68}-q^{66}-q^{64}-q^{62}-q^{60}-q^{58}-q^{54}+q^{46}+2q^{42}+2q^{38}+q^{36}+2q^{34}+q^{32}+2q^{30}+q^{28}+2q^{26}+2q^{22}+q^{18}+q^{14}$

B5 Invariants.

Weight	Invariant
1,0,0,0,0	$q^{120}-q^{98}-q^{94}-q^{90}-q^{86}-q^{84}-q^{82}-q^{80}-q^{78}-q^{76}-q^{74}-q^{70}-q^{66}+q^{58}+2q^{54}+2q^{50}+2q^{46}+q^{44}+2q^{42}+q^{40}+2q^{38}+q^{36}+2q^{34}+2q^{30}+2q^{26}+q^{22}+q^{18}$

C3 Invariants.

Weight	Invariant
1,0,0	$-q^{42}-q^{34}-q^{32}-q^{24}+q^{20}+2q^{18}+q^{16}+q^{14}+q^{12}+2q^{10}+q^{8}+q^{6}$

C4 Invariants.

Weight	Invariant
1,0,0,0	$-q^{54}-q^{44}-q^{42}-q^{40}-q^{32}-q^{30}+q^{26}+2q^{24}+2q^{22}+q^{20}+q^{18}+q^{16}+2q^{14}+2q^{12}+q^{10}+q^{8}$

D4 Invariants.

Weight	Invariant
0,1,0,0	$q^{72}-q^{64}-q^{62}+2q^{56}+4q^{54}+5q^{52}+4q^{50}+3q^{48}-q^{46}-5q^{44}-9q^{42}-13q^{40}-14q^{38}-13q^{36}-9q^{34}-4q^{32}+2q^{30}+7q^{28}+12q^{26}+12q^{24}+14q^{22}+11q^{20}+9q^{18}+6q^{16}+4q^{14}+q^{12}+q^{10}$
1,0,0,0	$q^{42}-q^{34}-q^{32}-2q^{30}-2q^{28}-2q^{26}-q^{24}+q^{20}+2q^{18}+3q^{16}+3q^{14}+3q^{12}+2q^{10}+q^{8}+q^{6}$

G2 Invariants.

Weight	Invariant
0,1	$q^{144}-q^{126}+q^{122}-q^{116}+2q^{112}+q^{110}-q^{108}+2q^{104}+q^{102}-q^{98}-q^{96}+q^{94}-2q^{90}-2q^{88}-q^{86}-q^{84}-2q^{82}-3q^{80}-2q^{78}-2q^{76}-2q^{74}-2q^{72}-2q^{70}-q^{68}-q^{64}-q^{62}+q^{60}+q^{58}+q^{56}+2q^{54}+q^{52}+2q^{50}+3q^{48}+2q^{46}+2q^{44}+3q^{42}+2q^{40}+2q^{38}+3q^{36}+2q^{34}+q^{32}+2q^{30}+q^{28}+q^{26}+q^{24}+q^{18}$
1,0	$q^{72}-q^{64}-q^{62}-q^{56}-2q^{54}-q^{52}+q^{50}-q^{46}-2q^{44}+2q^{40}+q^{38}-q^{36}+2q^{32}+2q^{30}+q^{28}+2q^{22}+2q^{20}+q^{14}+q^{12}+q^{10}$

.

Computer Talk[show]

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["3 1"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$t+t^{-1}-1$

In[5]:=

Conway[K][z]

Out[5]=

$z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 3, -2 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$-q^{-4}+q^{-3}+q^{-1}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$-a^{4}+a^{2}z^{2}+2a^{2}$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$a^{5}z+a^{4}z^{2}-a^{4}+a^{3}z+a^{2}z^{2}-2a^{2}$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {}

Computer Talk[show]

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["3 1"];

In[4]:=

{A = Alexander[K][t], J = Jones[K][q]}

KnotTheory::loading: Loading precomputed data in PD4Knots`.

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[4]=

{ $t+t^{-1}-1$, $-q^{-4}+q^{-3}+q^{-1}$ }

In[5]:=

DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]

KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.

KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

Out[5]=

{}

In[6]:=

DeleteCases[ Select[ AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) & ], K ]

KnotTheory::loading: Loading precomputed data in Jones4Knots11`.

Out[6]=

{}

Vassiliev invariants

V2 and V3:

(1, -1)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $4$ $-8$ $8$ ${\frac {62}{3}}$ ${\frac {10}{3}}$ $-32$ $-{\frac {176}{3}}$ $-{\frac {32}{3}}$ $-8$ ${\frac {32}{3}}$ $32$ ${\frac {248}{3}}$ ${\frac {40}{3}}$ ${\frac {5071}{30}}$ ${\frac {58}{15}}$ ${\frac {3062}{45}}$ ${\frac {17}{18}}$ ${\frac {271}{30}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$-2 is the signature of 3 1. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ -3 -2 -1 0 χ -1       1 1 -3       1 1 -5   1     1 -7         0 -9 1       -1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=-3$ $i=-1$ $r=-3$ ${\mathbb {Z} }$ $r=-2$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-1$ $r=0$ ${\mathbb {Z} }$ ${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the $n+1$-dimensional representation of $sl(2)$)[show]

$n$	$J_{n}$
2	$q^{-2}+q^{-5}-q^{-7}+q^{-8}-q^{-9}-q^{-10}+q^{-11}$
3	$q^{-3}+q^{-7}-q^{-10}+q^{-11}-q^{-13}-q^{-14}+q^{-15}-q^{-17}+q^{-19}+q^{-20}-q^{-21}$
4	$q^{-4}+q^{-9}-q^{-13}+q^{-14}-q^{-17}-q^{-18}+q^{-19}-q^{-22}-q^{-23}+2q^{-24}-q^{-28}+2q^{-29}-q^{-32}-q^{-33}+q^{-34}$
5	$q^{-5}+q^{-11}-q^{-16}+q^{-17}-q^{-21}-q^{-22}+q^{-23}-q^{-27}-q^{-28}+q^{-29}+q^{-30}-q^{-33}+q^{-35}+q^{-36}-q^{-39}+q^{-42}-q^{-44}-q^{-45}+q^{-48}+q^{-49}-q^{-50}$
6	$q^{-6}+q^{-13}-q^{-19}+q^{-20}-q^{-25}-q^{-26}+q^{-27}-q^{-32}-q^{-33}+q^{-34}+q^{-36}-q^{-39}-q^{-40}+2q^{-41}+q^{-43}-q^{-46}-q^{-47}+2q^{-48}-q^{-53}-2q^{-54}+2q^{-55}-q^{-60}-q^{-61}+2q^{-62}+q^{-64}-q^{-67}-q^{-68}+q^{-69}$
7	$q^{-7}+q^{-15}-q^{-22}+q^{-23}-q^{-29}-q^{-30}+q^{-31}-q^{-37}-q^{-38}+q^{-39}+q^{-42}-q^{-45}-q^{-46}+q^{-47}+q^{-48}+q^{-50}-q^{-53}-q^{-54}+q^{-55}+q^{-56}+q^{-58}-q^{-59}-q^{-61}-q^{-62}+q^{-63}+q^{-66}-q^{-67}-q^{-69}-q^{-70}+q^{-71}+q^{-73}+q^{-74}-q^{-75}-q^{-78}+q^{-79}+q^{-81}+q^{-82}-q^{-83}-q^{-84}-q^{-86}+q^{-89}+q^{-90}-q^{-91}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session, or any of the Computer Talk sections above.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Rolfsen Knot Page master template (intermediate). See/edit the Rolfsen_Splice_Base (expert). Back to the top.

0_1 4_1