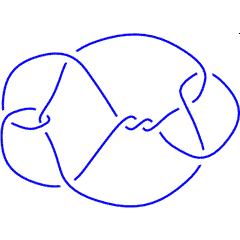
K11a109

K11a108

K11a110

(Knotscape image)	See the full Hoste-Thistlethwaite Table of 11 Crossing Knots. Visit K11a109 at Knotilus!

Knot presentations

Planar diagram presentation	X4251 X10,4,11,3 X14,5,15,6 X16,8,17,7 X2,10,3,9 X20,11,21,12 X22,13,1,14 X18,16,19,15 X8,18,9,17 X6,19,7,20 X12,21,13,22
Gauss code	1, -5, 2, -1, 3, -10, 4, -9, 5, -2, 6, -11, 7, -3, 8, -4, 9, -8, 10, -6, 11, -7
Dowker-Thistlethwaite code	4 10 14 16 2 20 22 18 8 6 12

A Braid Representative	{{{braid_table}}}
A Morse Link Presentation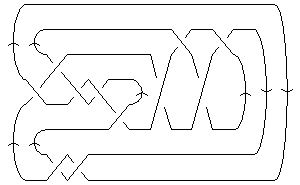

Three dimensional invariants

Symmetry type Reversible Unknotting number $\{1,2\}$ 3-genus 4 Bridge index 3 Super bridge index Missing Nakanishi index Missing Maximal Thurston-Bennequin number Data:K11a109/ThurstonBennequinNumber Hyperbolic Volume 15.1191 A-Polynomial See Data:K11a109/A-polynomial

[edit Notes for K11a109's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus Missing Topological 4 genus Missing Concordance genus $[2,4]$ Rasmussen s-Invariant 0

[edit Notes for K11a109's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$t^{4}-5t^{3}+14t^{2}-24t+29-24t^{-1}+14t^{-2}-5t^{-3}+t^{-4}$
Conway polynomial	$z^{8}+3z^{6}+4z^{4}+3z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 117, 0 }
Jones polynomial	$q^{6}-4q^{5}+7q^{4}-12q^{3}+17q^{2}-18q+19-16q^{-1}+12q^{-2}-7q^{-3}+3q^{-4}-q^{-5}$
HOMFLY-PT polynomial (db, data sources)	$z^{8}-a^{2}z^{6}-2z^{6}a^{-2}+6z^{6}-4a^{2}z^{4}-8z^{4}a^{-2}+z^{4}a^{-4}+15z^{4}-6a^{2}z^{2}-10z^{2}a^{-2}+2z^{2}a^{-4}+17z^{2}-3a^{2}-3a^{-2}+7$
Kauffman polynomial (db, data sources)	$z^{10}a^{-2}+z^{10}+4az^{9}+8z^{9}a^{-1}+4z^{9}a^{-3}+6a^{2}z^{8}+13z^{8}a^{-2}+6z^{8}a^{-4}+13z^{8}+5a^{3}z^{7}+az^{7}-9z^{7}a^{-1}-z^{7}a^{-3}+4z^{7}a^{-5}+3a^{4}z^{6}-9a^{2}z^{6}-42z^{6}a^{-2}-16z^{6}a^{-4}+z^{6}a^{-6}-37z^{6}+a^{5}z^{5}-7a^{3}z^{5}-11az^{5}-10z^{5}a^{-1}-18z^{5}a^{-3}-11z^{5}a^{-5}-5a^{4}z^{4}+9a^{2}z^{4}+46z^{4}a^{-2}+13z^{4}a^{-4}-2z^{4}a^{-6}+45z^{4}-2a^{5}z^{3}+3a^{3}z^{3}+13az^{3}+20z^{3}a^{-1}+19z^{3}a^{-3}+7z^{3}a^{-5}+2a^{4}z^{2}-8a^{2}z^{2}-22z^{2}a^{-2}-5z^{2}a^{-4}-27z^{2}+a^{5}z-a^{3}z-6az-8za^{-1}-4za^{-3}+3a^{2}+3a^{-2}+7$
The A2 invariant	$-q^{14}+q^{12}-3q^{10}+q^{8}+q^{6}-2q^{4}+5q^{2}-2+4q^{-2}+q^{-4}+3q^{-8}-4q^{-10}-q^{-14}-q^{-16}+q^{-18}$
The G2 invariant	$q^{80}-2q^{78}+5q^{76}-8q^{74}+9q^{72}-8q^{70}+q^{68}+13q^{66}-29q^{64}+47q^{62}-59q^{60}+53q^{58}-30q^{56}-20q^{54}+87q^{52}-151q^{50}+190q^{48}-184q^{46}+111q^{44}+17q^{42}-178q^{40}+321q^{38}-383q^{36}+329q^{34}-167q^{32}-75q^{30}+296q^{28}-427q^{26}+416q^{24}-248q^{22}-q^{20}+233q^{18}-340q^{16}+281q^{14}-81q^{12}-170q^{10}+352q^{8}-375q^{6}+215q^{4}+84q^{2}-392+602q^{-2}-592q^{-4}+372q^{-6}-11q^{-8}-369q^{-10}+626q^{-12}-669q^{-14}+501q^{-16}-172q^{-18}-178q^{-20}+435q^{-22}-489q^{-24}+346q^{-26}-84q^{-28}-187q^{-30}+334q^{-32}-310q^{-34}+123q^{-36}+138q^{-38}-351q^{-40}+438q^{-42}-346q^{-44}+100q^{-46}+172q^{-48}-392q^{-50}+469q^{-52}-393q^{-54}+203q^{-56}+24q^{-58}-208q^{-60}+303q^{-62}-291q^{-64}+199q^{-66}-76q^{-68}-33q^{-70}+95q^{-72}-115q^{-74}+96q^{-76}-55q^{-78}+22q^{-80}+7q^{-82}-18q^{-84}+17q^{-86}-14q^{-88}+7q^{-90}-3q^{-92}+q^{-94}$

Further Quantum Invariants

K11a109 Quantum Invariants.

Computer Talk

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["K11a109"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$t^{4}-5t^{3}+14t^{2}-24t+29-24t^{-1}+14t^{-2}-5t^{-3}+t^{-4}$

In[5]:=

Conway[K][z]

Out[5]=

$z^{8}+3z^{6}+4z^{4}+3z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 117, 0 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$q^{6}-4q^{5}+7q^{4}-12q^{3}+17q^{2}-18q+19-16q^{-1}+12q^{-2}-7q^{-3}+3q^{-4}-q^{-5}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$z^{8}-a^{2}z^{6}-2z^{6}a^{-2}+6z^{6}-4a^{2}z^{4}-8z^{4}a^{-2}+z^{4}a^{-4}+15z^{4}-6a^{2}z^{2}-10z^{2}a^{-2}+2z^{2}a^{-4}+17z^{2}-3a^{2}-3a^{-2}+7$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$z^{10}a^{-2}+z^{10}+4az^{9}+8z^{9}a^{-1}+4z^{9}a^{-3}+6a^{2}z^{8}+13z^{8}a^{-2}+6z^{8}a^{-4}+13z^{8}+5a^{3}z^{7}+az^{7}-9z^{7}a^{-1}-z^{7}a^{-3}+4z^{7}a^{-5}+3a^{4}z^{6}-9a^{2}z^{6}-42z^{6}a^{-2}-16z^{6}a^{-4}+z^{6}a^{-6}-37z^{6}+a^{5}z^{5}-7a^{3}z^{5}-11az^{5}-10z^{5}a^{-1}-18z^{5}a^{-3}-11z^{5}a^{-5}-5a^{4}z^{4}+9a^{2}z^{4}+46z^{4}a^{-2}+13z^{4}a^{-4}-2z^{4}a^{-6}+45z^{4}-2a^{5}z^{3}+3a^{3}z^{3}+13az^{3}+20z^{3}a^{-1}+19z^{3}a^{-3}+7z^{3}a^{-5}+2a^{4}z^{2}-8a^{2}z^{2}-22z^{2}a^{-2}-5z^{2}a^{-4}-27z^{2}+a^{5}z-a^{3}z-6az-8za^{-1}-4za^{-3}+3a^{2}+3a^{-2}+7$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {K11a44, K11a47,}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {}

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["K11a109"];

In[4]:=

{A = Alexander[K][t], J = Jones[K][q]}

KnotTheory::loading: Loading precomputed data in PD4Knots`.

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[4]=

{ $t^{4}-5t^{3}+14t^{2}-24t+29-24t^{-1}+14t^{-2}-5t^{-3}+t^{-4}$, $q^{6}-4q^{5}+7q^{4}-12q^{3}+17q^{2}-18q+19-16q^{-1}+12q^{-2}-7q^{-3}+3q^{-4}-q^{-5}$ }

In[5]:=

DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]

KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.

KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

Out[5]=

{K11a44, K11a47,}

In[6]:=

DeleteCases[ Select[ AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) & ], K ]

KnotTheory::loading: Loading precomputed data in Jones4Knots11`.

Out[6]=

{}

Vassiliev invariants

V2 and V3:

(3, 0)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $12$ $0$ $72$ $78$ $2$ $0$ $32$ $32$ $0$ $288$ $0$ $936$ $24$ ${\frac {9151}{10}}$ ${\frac {1894}{15}}$ ${\frac {794}{5}}$ ${\frac {11}{2}}$ ${\frac {31}{10}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$0 is the signature of K11a109. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ -5 -4 -3 -2 -1 0 1 2 3 4 5 6 χ 13                       1 1 11                     3   -3 9                   4 1   3 7                 8 3     -5 5               9 4       5 3             9 8         -1 1           10 9           1 -1         7 10             3 -3       5 9               -4 -5     2 7                 5 -7   1 5                   -4 -9   2                     2 -11 1                       -1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=-1$ $i=1$ $r=-5$ ${\mathbb {Z} }$ $r=-4$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-3$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=-2$ ${\mathbb {Z} }^{7}\oplus {\mathbb {Z} }_{2}^{5}$ ${\mathbb {Z} }^{5}$ $r=-1$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{7}$ ${\mathbb {Z} }^{7}$ $r=0$ ${\mathbb {Z} }^{10}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{10}$ $r=1$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=2$ ${\mathbb {Z} }^{8}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=3$ ${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{8}$ ${\mathbb {Z} }^{8}$ $r=4$ ${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}^{4}$ ${\mathbb {Z} }^{4}$ $r=5$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=6$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages. See/edit the Hoste-Thistlethwaite Knot Page master template (intermediate). See/edit the Hoste-Thistlethwaite_Splice_Base (expert). Back to the top.

K11a108 K11a110