(For In[1] see Setup)
| In[2]:=
|
?Vassiliev
|
| Vassiliev[2][K] computes the (standardly normalized) type 2 Vassiliev invariant of the knot K, i.e., the coefficient of z^2 in Conway[K][z]. Vassiliev[3][K] computes the (standardly normalized) type 3 Vassiliev invariant of the knot K, i.e., 3J''(1)-(1/36)J'''(1) where J is the Jones polynomial of K.
|
|
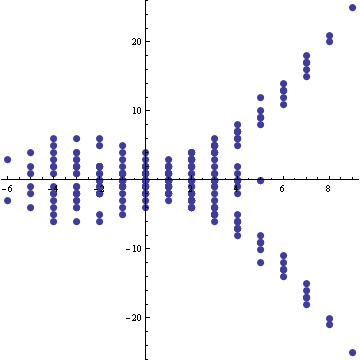
Thus, for example, let us reproduce Willerton's "fish" (arXiv:math.GT/0104061), the result of plotting the values of  against the values of
against the values of  , where
, where  is the (standardly normalized) type 2 invariant of
is the (standardly normalized) type 2 invariant of  ,
,  is the (standardly normalized) type 3 invariant of
is the (standardly normalized) type 3 invariant of  , and where
, and where  runs over a set of knots with equal crossing numbers (10, in the example below):
runs over a set of knots with equal crossing numbers (10, in the example below):
In[3]:=
|
ListPlot[
Join @@ Table[
K = Knot[10, k] ; v2 = Vassiliev[2][K]; v3 = Vassiliev[3][K];
{{v2, v3}, {v2, -v3}},
{k, 165}
],
PlotStyle -> PointSize[0.02], PlotRange -> All, AspectRatio -> 1
]
|
|
|
|
Out[3]=
|
-Graphics-
|




