10 124

10_123

10_125

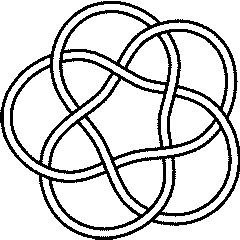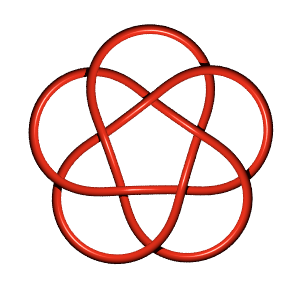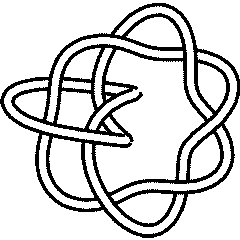
(KnotPlot image)	See the full Rolfsen Knot Table. Visit 10 124's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 10 124 at Knotilus!
	10_124 is also known as the torus knot T(5,3) or the pretzel knot P(5,3,-2). It is one of two knots which are both torus knots and pretzel knots, the other being 8_19 = T(4,3) = P(3,3,-2).

If one takes the symmetric diagram for 10_123 and makes it doubly alternating one gets a diagram for 10_124. That's the torus knot view. There is then a nice representation of the quandle of 10_124 into the dodecahedral quandle $Q_{30}$. See [1].

10_124 is not $k$-colourable for any $k$. See The Determinant and the Signature.

Torus knot T(5,3) form

Knot presentations

Planar diagram presentation	X4251 X8493 X9,17,10,16 X5,15,6,14 X15,7,16,6 X11,19,12,18 X13,1,14,20 X17,11,18,10 X19,13,20,12 X2837
Gauss code	1, -10, 2, -1, -4, 5, 10, -2, -3, 8, -6, 9, -7, 4, -5, 3, -8, 6, -9, 7
Dowker-Thistlethwaite code	4 8 -14 2 -16 -18 -20 -6 -10 -12
Conway Notation	[5,3,2-]

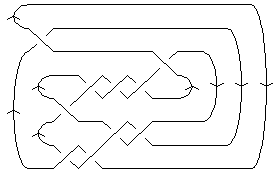
Minimum Braid Representative	A Morse Link Presentation	An Arc Presentation
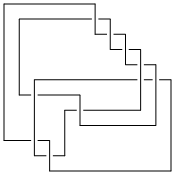
Length is 10, width is 3, Braid index is 3		[{4, 12}, {3, 5}, {1, 4}, {6, 11}, {5, 10}, {2, 6}, {12, 3}, {11, 9}, {10, 8}, {9, 7}, {8, 2}, {7, 1}]

[edit Notes on presentations of 10 124]

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.org/wiki/KnotTheory.

In[3]:=

K = Knot["10 124"];

In[4]:=

PD[K]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

X4251 X8493 X9,17,10,16 X5,15,6,14 X15,7,16,6 X11,19,12,18 X13,1,14,20 X17,11,18,10 X19,13,20,12 X2837

In[5]:=

GaussCode[K]

Out[5]=

1, -10, 2, -1, -4, 5, 10, -2, -3, 8, -6, 9, -7, 4, -5, 3, -8, 6, -9, 7

In[6]:=

DTCode[K]

Out[6]=

4 8 -14 2 -16 -18 -20 -6 -10 -12

(The path below may be different on your system)

In[7]:=

AppendTo[$Path, "C:/bin/LinKnot/"];

In[8]:=

ConwayNotation[K]

Out[8]=

[5,3,2-]

In[9]:=

br = BR[K]

KnotTheory::credits: The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See arXiv:math.GT/0401051.

Out[9]=

${\textrm {BR}}(3,\{1,1,1,1,1,2,1,1,1,2\})$

In[10]:=

{First[br], Crossings[br], BraidIndex[K]}

KnotTheory::credits: The braid index data known to KnotTheory` is taken from Charles Livingston's http://www.indiana.edu/~knotinfo/.

KnotTheory::loading: Loading precomputed data in IndianaData`.

Out[10]=

{ 3, 10, 3 }

In[11]:=

Show[BraidPlot[br]]

Out[11]=

-Graphics-

In[12]:=

Show[DrawMorseLink[K]]

KnotTheory::credits: "MorseLink was added to KnotTheory` by Siddarth Sankaran at the University of Toronto in the summer of 2005."

KnotTheory::credits: "DrawMorseLink was written by Siddarth Sankaran at the University of Toronto in the summer of 2005."

Out[12]=

-Graphics-

In[13]:=

ap = ArcPresentation[K]

Out[13]=

ArcPresentation[{4, 12}, {3, 5}, {1, 4}, {6, 11}, {5, 10}, {2, 6}, {12, 3}, {11, 9}, {10, 8}, {9, 7}, {8, 2}, {7, 1}]

In[14]:=

Draw[ap]

Out[14]=

-Graphics-

Three dimensional invariants

Symmetry type Reversible Unknotting number 4 3-genus 4 Bridge index 3 Super bridge index Missing Nakanishi index 1 Maximal Thurston-Bennequin number [7][-15] Hyperbolic Volume Not hyperbolic A-Polynomial See Data:10 124/A-polynomial

[edit Notes for 10 124's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus $4$ Topological 4 genus $4$ Concordance genus $4$ Rasmussen s-Invariant -8

[edit Notes for 10 124's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$t^{4}-t^{3}+t-1+t^{-1}-t^{-3}+t^{-4}$
Conway polynomial	$z^{8}+7z^{6}+14z^{4}+8z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 1, 8 }
Jones polynomial	$-q^{10}+q^{6}+q^{4}$
HOMFLY-PT polynomial (db, data sources)	$z^{8}a^{-8}+8z^{6}a^{-8}-z^{6}a^{-10}+21z^{4}a^{-8}-7z^{4}a^{-10}+21z^{2}a^{-8}-14z^{2}a^{-10}+z^{2}a^{-12}+7a^{-8}-8a^{-10}+2a^{-12}$
Kauffman polynomial (db, data sources)	$z^{8}a^{-8}+z^{8}a^{-10}+z^{7}a^{-9}+z^{7}a^{-11}-8z^{6}a^{-8}-8z^{6}a^{-10}-7z^{5}a^{-9}-7z^{5}a^{-11}+21z^{4}a^{-8}+21z^{4}a^{-10}+14z^{3}a^{-9}+14z^{3}a^{-11}-21z^{2}a^{-8}-22z^{2}a^{-10}-z^{2}a^{-12}-8za^{-9}-8za^{-11}+7a^{-8}+8a^{-10}+2a^{-12}$
The A2 invariant	$q^{-14}+q^{-16}+2q^{-18}+2q^{-20}+2q^{-22}+q^{-24}-2q^{-28}-2q^{-30}-2q^{-32}-q^{-34}+q^{-40}$
The G2 invariant	$q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}+2q^{-80}+2q^{-82}+q^{-84}+2q^{-86}+2q^{-88}+2q^{-90}+2q^{-92}+2q^{-94}+q^{-96}+2q^{-98}+q^{-100}+q^{-104}+q^{-106}-q^{-112}-q^{-114}-q^{-118}-2q^{-120}-2q^{-122}-q^{-124}-q^{-126}-2q^{-128}-2q^{-130}-2q^{-132}-q^{-134}-q^{-136}-2q^{-138}-2q^{-140}-q^{-142}-q^{-146}-q^{-148}+q^{-160}+q^{-162}+q^{-168}+q^{-170}+q^{-180}$

Further Quantum Invariants

Further quantum knot invariants for 10_124.

A1 Invariants.

Weight	Invariant
1	$q^{-7}+q^{-9}+q^{-11}+q^{-13}-q^{-19}-q^{-21}$
2	$q^{-14}+q^{-16}+q^{-18}+q^{-20}+q^{-22}+q^{-24}+q^{-26}-q^{-36}-q^{-38}-q^{-40}-q^{-42}-q^{-44}+q^{-60}$
3	$q^{-21}+q^{-23}+q^{-25}+q^{-27}+q^{-29}+q^{-31}+q^{-33}+q^{-35}+q^{-37}+q^{-39}-q^{-53}-q^{-55}-q^{-57}-q^{-59}-q^{-61}-q^{-63}-q^{-65}-q^{-67}+q^{-97}+q^{-99}+q^{-101}+q^{-103}-q^{-109}-q^{-111}$
5	$q^{-35}+q^{-37}+q^{-39}+q^{-41}+q^{-43}+q^{-45}+q^{-47}+q^{-49}+q^{-51}+q^{-53}+q^{-55}+q^{-57}+q^{-59}+q^{-61}+q^{-63}+q^{-65}-q^{-87}-q^{-89}-q^{-91}-q^{-93}-q^{-95}-q^{-97}-q^{-99}-q^{-101}-q^{-103}-q^{-105}-q^{-107}-q^{-109}-q^{-111}-q^{-113}+q^{-171}+q^{-173}+q^{-175}+q^{-177}+q^{-179}+q^{-181}+q^{-183}+q^{-185}+q^{-187}+q^{-189}-q^{-203}-q^{-205}-q^{-207}-q^{-209}-q^{-211}-q^{-213}-q^{-215}-q^{-217}+q^{-247}+q^{-249}+q^{-251}+q^{-253}-q^{-259}-q^{-261}$
6	$q^{-42}+q^{-44}+q^{-46}+q^{-48}+q^{-50}+q^{-52}+q^{-54}+q^{-56}+q^{-58}+q^{-60}+q^{-62}+q^{-64}+q^{-66}+q^{-68}+q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}-q^{-104}-q^{-106}-q^{-108}-q^{-110}-q^{-112}-q^{-114}-q^{-116}-q^{-118}-q^{-120}-q^{-122}-q^{-124}-q^{-126}-q^{-128}-q^{-130}-q^{-132}-q^{-134}-q^{-136}+q^{-208}+q^{-210}+q^{-212}+q^{-214}+q^{-216}+q^{-218}+q^{-220}+q^{-222}+q^{-224}+q^{-226}+q^{-228}+q^{-230}+q^{-232}-q^{-250}-q^{-252}-q^{-254}-q^{-256}-q^{-258}-q^{-260}-q^{-262}-q^{-264}-q^{-266}-q^{-268}-q^{-270}+q^{-314}+q^{-316}+q^{-318}+q^{-320}+q^{-322}+q^{-324}+q^{-326}-q^{-336}-q^{-338}-q^{-340}-q^{-342}-q^{-344}+q^{-360}$

A2 Invariants.

Weight	Invariant
1,0	$q^{-14}+q^{-16}+2q^{-18}+2q^{-20}+2q^{-22}+q^{-24}-2q^{-28}-2q^{-30}-2q^{-32}-q^{-34}+q^{-40}$
1,1	$q^{-28}+2q^{-30}+4q^{-32}+6q^{-34}+7q^{-36}+8q^{-38}+6q^{-40}+4q^{-42}+q^{-44}-2q^{-46}-6q^{-48}-8q^{-50}-9q^{-52}-8q^{-54}-6q^{-56}-4q^{-58}-2q^{-60}+2q^{-64}+2q^{-66}+4q^{-68}+4q^{-70}+4q^{-72}+2q^{-74}+q^{-76}-2q^{-78}-2q^{-80}-2q^{-82}-q^{-84}+2q^{-90}$
2,0	$q^{-28}+q^{-30}+2q^{-32}+2q^{-34}+3q^{-36}+3q^{-38}+4q^{-40}+3q^{-42}+3q^{-44}+2q^{-46}+2q^{-48}-q^{-52}-3q^{-54}-4q^{-56}-5q^{-58}-5q^{-60}-5q^{-62}-4q^{-64}-3q^{-66}-2q^{-68}-q^{-70}+2q^{-74}+2q^{-76}+4q^{-78}+4q^{-80}+4q^{-82}+2q^{-84}+q^{-86}-2q^{-88}-2q^{-90}-2q^{-92}-q^{-94}+q^{-100}$

A3 Invariants.

Weight	Invariant
0,1,0	$q^{-28}+q^{-30}+3q^{-32}+4q^{-34}+6q^{-36}+6q^{-38}+7q^{-40}+3q^{-42}+q^{-44}-4q^{-46}-7q^{-48}-9q^{-50}-9q^{-52}-6q^{-54}-3q^{-56}+q^{-58}+3q^{-60}+4q^{-62}+2q^{-64}+2q^{-66}$
1,0,0	$q^{-21}+q^{-23}+2q^{-25}+3q^{-27}+3q^{-29}+3q^{-31}+2q^{-33}-2q^{-37}-3q^{-39}-4q^{-41}-3q^{-43}-2q^{-45}+q^{-49}+q^{-51}+q^{-53}$
1,0,1	$q^{-42}+2q^{-44}+5q^{-46}+9q^{-48}+14q^{-50}+19q^{-52}+23q^{-54}+22q^{-56}+19q^{-58}+10q^{-60}-q^{-62}-14q^{-64}-26q^{-66}-34q^{-68}-38q^{-70}-35q^{-72}-26q^{-74}-13q^{-76}-q^{-78}+11q^{-80}+18q^{-82}+21q^{-84}+19q^{-86}+14q^{-88}+8q^{-90}+4q^{-92}-3q^{-96}-3q^{-98}-4q^{-100}-3q^{-102}-3q^{-104}-q^{-106}-q^{-108}+2q^{-120}$

A4 Invariants.

Weight	Invariant
0,1,0,0	$q^{-42}+q^{-44}+3q^{-46}+5q^{-48}+8q^{-50}+10q^{-52}+14q^{-54}+13q^{-56}+13q^{-58}+8q^{-60}+2q^{-62}-7q^{-64}-14q^{-66}-21q^{-68}-23q^{-70}-21q^{-72}-16q^{-74}-8q^{-76}-q^{-78}+7q^{-80}+9q^{-82}+11q^{-84}+9q^{-86}+7q^{-88}+3q^{-90}+2q^{-92}-q^{-96}-q^{-98}-q^{-100}-q^{-102}-q^{-104}$
1,0,0,0	$q^{-28}+q^{-30}+2q^{-32}+3q^{-34}+4q^{-36}+4q^{-38}+4q^{-40}+2q^{-42}+q^{-44}-2q^{-46}-4q^{-48}-5q^{-50}-5q^{-52}-4q^{-54}-2q^{-56}+q^{-60}+2q^{-62}+q^{-64}+q^{-66}$

B2 Invariants.

Weight	Invariant
0,1	$q^{-28}+q^{-30}+q^{-32}+2q^{-34}+2q^{-36}+2q^{-38}+q^{-40}+q^{-42}+q^{-44}-q^{-48}-q^{-50}-q^{-52}-2q^{-54}-q^{-56}-q^{-58}-q^{-60}$
1,0	$q^{-42}+q^{-46}+q^{-48}+2q^{-50}+q^{-52}+3q^{-54}+2q^{-56}+3q^{-58}+2q^{-60}+3q^{-62}+2q^{-64}+2q^{-66}-q^{-72}-2q^{-74}-3q^{-76}-3q^{-78}-3q^{-80}-4q^{-82}-3q^{-84}-3q^{-86}-2q^{-88}-2q^{-90}+q^{-96}+q^{-98}+2q^{-100}+q^{-102}+q^{-104}+q^{-106}+q^{-108}$

D4 Invariants.

Weight	Invariant
1,0,0,0	$q^{-42}+q^{-44}+2q^{-46}+4q^{-48}+5q^{-50}+7q^{-52}+8q^{-54}+8q^{-56}+7q^{-58}+5q^{-60}+q^{-62}-3q^{-64}-7q^{-66}-10q^{-68}-11q^{-70}-11q^{-72}-9q^{-74}-6q^{-76}-2q^{-78}+q^{-80}+3q^{-82}+4q^{-84}+4q^{-86}+3q^{-88}+2q^{-90}+q^{-92}$

G2 Invariants.

Weight	Invariant
1,0	$q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}+2q^{-80}+2q^{-82}+q^{-84}+2q^{-86}+2q^{-88}+2q^{-90}+2q^{-92}+2q^{-94}+q^{-96}+2q^{-98}+q^{-100}+q^{-104}+q^{-106}-q^{-112}-q^{-114}-q^{-118}-2q^{-120}-2q^{-122}-q^{-124}-q^{-126}-2q^{-128}-2q^{-130}-2q^{-132}-q^{-134}-q^{-136}-2q^{-138}-2q^{-140}-q^{-142}-q^{-146}-q^{-148}+q^{-160}+q^{-162}+q^{-168}+q^{-170}+q^{-180}$

.

Computer Talk

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["10 124"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$t^{4}-t^{3}+t-1+t^{-1}-t^{-3}+t^{-4}$

In[5]:=

Conway[K][z]

Out[5]=

$z^{8}+7z^{6}+14z^{4}+8z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 1, 8 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$-q^{10}+q^{6}+q^{4}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$z^{8}a^{-8}+8z^{6}a^{-8}-z^{6}a^{-10}+21z^{4}a^{-8}-7z^{4}a^{-10}+21z^{2}a^{-8}-14z^{2}a^{-10}+z^{2}a^{-12}+7a^{-8}-8a^{-10}+2a^{-12}$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$z^{8}a^{-8}+z^{8}a^{-10}+z^{7}a^{-9}+z^{7}a^{-11}-8z^{6}a^{-8}-8z^{6}a^{-10}-7z^{5}a^{-9}-7z^{5}a^{-11}+21z^{4}a^{-8}+21z^{4}a^{-10}+14z^{3}a^{-9}+14z^{3}a^{-11}-21z^{2}a^{-8}-22z^{2}a^{-10}-z^{2}a^{-12}-8za^{-9}-8za^{-11}+7a^{-8}+8a^{-10}+2a^{-12}$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {}

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["10 124"];

In[4]:=

{A = Alexander[K][t], J = Jones[K][q]}

KnotTheory::loading: Loading precomputed data in PD4Knots`.

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[4]=

{ $t^{4}-t^{3}+t-1+t^{-1}-t^{-3}+t^{-4}$, $-q^{10}+q^{6}+q^{4}$ }

In[5]:=

DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]

KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.

KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

Out[5]=

{}

In[6]:=

DeleteCases[ Select[ AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) & ], K ]

KnotTheory::loading: Loading precomputed data in Jones4Knots11`.

Out[6]=

{}

Vassiliev invariants

V2 and V3:

(8, 20)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $32$ $160$ $512$ ${\frac {3184}{3}}$ ${\frac {416}{3}}$ $5120$ ${\frac {23680}{3}}$ ${\frac {4000}{3}}$ $832$ ${\frac {16384}{3}}$ $12800$ ${\frac {101888}{3}}$ ${\frac {13312}{3}}$ ${\frac {910684}{15}}$ ${\frac {59264}{15}}$ ${\frac {869536}{45}}$ ${\frac {2756}{9}}$ ${\frac {34684}{15}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$8 is the signature of 10 124. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ 0 1 2 3 4 5 6 7 χ 21               1 -1 19           1     -1 17           1 1   0 15       1 1       0 13         1       1 11     1           1 9 1               1 7 1               1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=5$ $i=7$ $i=9$ $r=0$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=1$ $r=2$ ${\mathbb {Z} }$ $r=3$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=4$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=5$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=6$ ${\mathbb {Z} }$ $r=7$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the $n+1$-dimensional representation of $sl(2)$)

$n$	$J_{n}$
2	$q^{29}-q^{28}+q^{26}-q^{25}+q^{23}-q^{22}-q^{21}+q^{20}-q^{19}-q^{18}+q^{17}-q^{15}+q^{14}+q^{11}+q^{8}$
3	$-q^{54}+q^{52}+q^{48}-q^{46}+q^{44}-q^{42}+q^{40}-q^{38}+q^{36}-q^{34}-q^{30}-q^{26}+q^{24}-q^{22}+q^{20}+q^{16}+q^{12}$
4	$q^{88}-q^{87}+q^{83}-q^{82}-q^{80}+q^{78}-q^{77}+q^{73}-q^{72}+q^{71}+q^{68}-q^{67}+q^{66}-q^{64}+q^{63}-q^{62}+q^{61}-q^{59}+q^{58}-q^{57}+q^{56}-q^{54}+q^{53}-q^{52}+q^{51}-q^{49}+q^{48}-q^{47}+q^{46}-q^{44}-q^{42}+q^{41}-q^{39}-q^{37}+q^{36}-q^{34}+q^{31}-q^{29}+q^{26}+q^{21}+q^{16}$
5	$-q^{128}+q^{126}+q^{124}-q^{122}+q^{118}-q^{116}+q^{112}-q^{110}-q^{104}+q^{92}+q^{86}-q^{82}+q^{80}-q^{76}+q^{74}-q^{70}+q^{68}-q^{64}+q^{62}-q^{58}+q^{56}-q^{54}-q^{52}+q^{50}-q^{48}-q^{46}+q^{44}-q^{42}+q^{38}-q^{36}+q^{32}+q^{26}+q^{20}$
6	$q^{177}-q^{176}+q^{170}-2q^{169}+q^{164}+q^{163}-2q^{162}+q^{160}+q^{157}+q^{156}-2q^{155}+q^{150}+q^{149}-2q^{148}+q^{143}+q^{142}-2q^{141}+q^{136}+q^{135}-2q^{134}-q^{132}+q^{129}+q^{128}-2q^{127}-q^{125}+q^{122}+2q^{121}-2q^{120}-q^{118}+q^{115}+2q^{114}-q^{113}-q^{111}+q^{108}+2q^{107}-q^{106}-q^{104}+q^{101}+q^{100}-q^{99}-q^{97}+q^{94}+q^{93}-q^{92}-q^{90}+q^{87}+q^{86}-q^{85}-q^{83}+q^{80}+q^{79}-q^{78}-q^{76}+q^{73}+q^{72}-q^{71}-q^{69}+q^{66}-q^{64}-q^{62}+q^{59}-q^{57}-q^{55}+q^{52}-q^{50}+q^{45}-q^{43}+q^{38}+q^{31}+q^{24}$
7	$-q^{232}+q^{230}+q^{228}-2q^{224}+q^{222}+q^{220}-2q^{216}+q^{214}+q^{212}-q^{210}-2q^{208}+q^{206}+q^{204}-2q^{200}+q^{198}+2q^{196}-2q^{192}+q^{190}+2q^{188}-q^{186}-2q^{184}+q^{182}+2q^{180}-q^{178}-2q^{176}+q^{174}+2q^{172}-q^{170}-2q^{168}+q^{166}+2q^{164}-q^{162}-2q^{160}+2q^{156}-q^{154}-2q^{152}+2q^{148}-q^{146}-q^{144}+2q^{140}-q^{138}-q^{136}+q^{134}+2q^{132}-q^{130}-q^{128}+q^{126}+2q^{124}-q^{122}-q^{120}+2q^{116}-q^{114}-q^{112}+2q^{108}-q^{106}-q^{104}+2q^{100}-q^{98}-q^{96}+2q^{92}-q^{90}-q^{88}+2q^{84}-q^{82}-q^{80}+q^{76}-q^{74}-q^{72}+q^{68}-q^{66}-q^{64}+q^{60}-q^{58}+q^{52}-q^{50}+q^{44}+q^{36}+q^{28}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session, or any of the Computer Talk sections above.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Rolfsen Knot Page master template (intermediate). See/edit the Rolfsen_Splice_Base (expert). Back to the top.

10_123 10_125