Finite Type (Vassiliev) Invariants

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

In[2]:= ?Vassiliev Vassiliev[2][K] computes the (standardly normalized) type 2 Vassiliev invariant of the knot K, i.e., the coefficient of z^2 in Conway[K][z]. Vassiliev[3][K] computes the (standardly normalized) type 3 Vassiliev invariant of the knot K, i.e., 3J''(1)-(1/36)J'''(1) where J is the Jones polynomial of K.

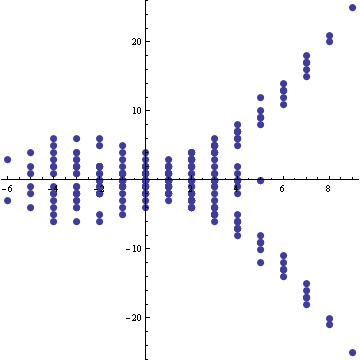
Thus, for example, let us reproduce Willerton's "fish" (arXiv:math.GT/0104061), the result of plotting the values of $V_2(K)$ against the values of $\pm V_3(K)$, where $V_2(K)$ is the (standardly normalized) type 2 invariant of $K$, $V_3(K)$ is the (standardly normalized) type 3 invariant of $K$, and where $K$ runs over a set of knots with equal crossing numbers (10, in the example below):

In[3]:=	ListPlot[ Join @@ Table[ K = Knot[10, k] ; v2 = Vassiliev[2][K]; v3 = Vassiliev[3][K]; {{v2, v3}, {v2, -v3}}, {k, 165} ], PlotStyle -> PointSize[0.02], PlotRange -> All, AspectRatio -> 1 ]
Out[3]=	-Graphics-

As another example, let us consider the expansion of the Jones polynomial for a knot $K$ as a power series in $x$ when we substitute the standard variable $q$ with $e^x$ and use the power series expansion of $e^x$:

$J(K)(q=e^x)=\sum_{n=0}^\infty\ V_n(K)x^n$

Then, for the above coefficients we have that $V_0(K)=1$ and for all $n\ge 1$ $V_n$ is a Vassiliev invariant of type $n$ [BirmanLin]. We can see this result by using the invariant formula:

$V\left(\doublepoint\right)= V\left(\overcrossing\right)-V\left(\undercrossing\right)$

to check the Birman-Lin condition, which tells us that an invariant $V$ is of type $m$ if it vanishes on knots with more than $m$ double points, or self intersections (see [Bar-Natan]). Computing $V$ on knots with more than one double point by resolving one self intersection at a time, it is enough to check that $V$ vanishes on knots with $m+1$ double points:

$V\underbrace{ \left(\doublepoint\cdots\doublepoint\right) }_{m+1}=0$

The following two programs let us determine $V_n(K)$ for any integer $n$ and knot $K$:

In[4]:=

SetCrossing[K_, l_Integer, s_] := Module[ {pd, n}, pd = PD[K]; If[PositiveQ[pd[[l]]], If[s == "-", pd[[l]] = RotateRight@pd[[l]]], If[s == "+", pd[[l]] = RotateLeft@pd[[l]]]]; pd];

In[5]:=

V[K_, n_] := Series[Jones[K][Exp[x]], {x, 0, n}]; V[K_, n_, {i1_, is___}] := V[SetCrossing[K, i1, "+"], n, {is}] - V[SetCrossing[K, i1, "-"], n, {is}]; V[K_, n_, {}] := V[K, n];

The first program, SetCrossing, sets the $l^{th}$ crossing of a knot $K$ to be positive or negative depending on whether we choose $s$ to be "$+$" or "$-$". The second program uses the invariant formula to give the series expansion of the Jones polynomial of a knot $K$ discussed above, up to order $x^n$, where a selected list of the crossings of $K$ are taken as double points. $V_n(K)$ is then the coefficient of the term containing $x^n$.

For example, we can check that $V_4$ disappears on the knot 9_47 with its first five crossings taken as double points:

In[6]:=	V[Knot[9, 47], 4, {1, 2, 3, 4, 5}]
Out[6]=	V[Knot[9, 47], 4, {1, 2, 3, 4, 5}]

The knot 9_47 with its first five crossings taken as double points.

[Bar-Natan] ^ D. Bar-Natan, On the Vassiliev Knot Invariants, Topology 34 (1995) 423-472.

[BirmanLin] ^ J.S. Birman and X.-S. Lin, Knot Polynomials and Vassiliev's Invariants, Invent. Math. 111 (1993) 225-270.