Cabling

From Knot Atlas

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

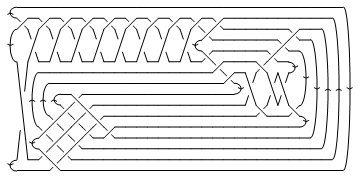
CableComponent[BR[n,js],K], whose code is available here, returns the n-th cable of the knot K with the braid on n strands with crossings js = {j1, j2, ...} inserted in it. It also performs the necessary number of 1 / n-twists on the components of the cable to compensate for a non-zero writhe number of the original knot. Cabling knot 3_1, for instance, and inserting the braid BR[3,{1,2}], we get:

(For In[1] see Setup)

In[2]:=

Import["http://katlas.org/wiki/CableComponent.m&action=raw"];

In[3]:=	CableComponent[BR[3, {1, 2}], Knot[3, 1]] // DrawMorseLink
Out[3]=	-Graphics-

For some special cases, we can check our result using Burau's Theorem.