Khovanov Homology
(See also: Tweaking JavaKh)
The Khovanov Homology of a knot or a link , also known as Khovanov's categorification of the Jones polynomial of , was defined by Khovanov in [Khovanov1] (also check [Bar-Natan1]), where the notation is closer to the notation used here). It is a graded homology theory; each homology group is in itself a direct sum of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" (which deserves the name "the Khovanov polynomial of "),
(For In[1] see Setup)
| ||||
Thus for example, here's the Khovanov polynomial of the knot 5_1:
In[3]:=
|
kh = Kh[Knot[5, 1]][q, t]
|
Out[3]=
|
-5 -3 1 1 1 1
q + q + ------ + ------ + ------ + -----
15 5 11 4 11 3 7 2
q t q t q t q t
|
The Euler characteristic of the Khovanov Homology is (up to normalization) the Jones polynomial of . Precisely,
Let us verify this in the case of 5_1:
In[4]:=
|
{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}
|
Out[4]=
|
-15 -7 -5 -3 -15 -7 -5 -3
{-q + q + q + q , -q + q + q + q }
|
 5_1 |
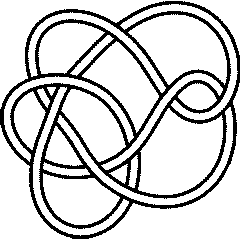 10_132 |
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, though :
In[5]:=
|
{
Jones[Knot[5, 1]] === Jones[Knot[10, 132]],
Kh[Knot[5, 1]] === Kh[Knot[10, 132]]
}
|
Out[5]=
|
{True, False}
|
The algorithm presently used by KnotTheory` is an efficient algorithm modeled on the Kauffman bracket algorithm of The Jones Polynomial, as explained in [Bar-Natan3] (which follows [Bar-Natan2]). Currently, two implementations of this algorithm are available:
- FastKh: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax
Kh[L, Program -> "FastKh"][q, t]or by changing the default behaviour ofKhby evaluatingSetOptions[Kh, Program -> "FastKh"]. - JavaKh: In the summer of 2005 Jeremy Green re-implemented the algorithm in java (java 1.5 required, can be had from http://java.sun.com/) with much further care to the details, leading to an improvement factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax
Kh[L, Program -> "JavaKh"][q, t].
In[6]:=
|
Options[Kh]
|
Out[6]=
|
{ExpansionOrder -> Automatic, Program -> JavaKh-v2, Modulus -> 0,
KnotTheory`FastKh`Universal -> False, JavaOptions -> }
|
JavaKh takes an additional option, Modulus, which sets the characteristic of the ground field for the homology computations to or to a prime . Thus for example, the following four In lines imply that the Khovanov homology of the torus knot T(6,5) has both 3 torsion and 5 torsion, but no 7 torsion:
In[7]:=
|
T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];
|
In[8]:=
|
Kh[T65, Modulus -> 3][q, t] - kh
|
Out[8]=
|
43 13 43 14
q t + q t
|
In[9]:=
|
Kh[T65, Modulus -> 5][q, t] - kh
|
Out[9]=
|
35 10 35 11 39 11 39 12
q t + q t + q t + q t
|
In[10]:=
|
Kh[T65, Modulus -> 7][q, t] - kh
|
Out[10]=
|
0
|
 T(6,5) |
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion:
| ||||
In[12]:=
|
SetOptions[Kh, JavaOptions -> "-Xmx256m"];
|
In[13]:=
|
T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];
|
In[14]:=
|
Factor[Kh[T87, Modulus -> 3][q, t] - kh]
|
Out[14]=
|
79 25
q t (1 + t)
|
In[15]:=
|
Factor[Kh[T87, Modulus -> 5][q, t] - kh]
|
Out[15]=
|
61 11 12 10 14 12 18 13
q t (1 + t) (1 + q t + q t + q t )
|
In[16]:=
|
Factor[Kh[T87, Modulus -> 7][q, t] - kh]
|
Out[16]=
|
61 14 8 6 12 7 10 8 14 9
q t (1 + t) (1 + q t + q t + q t + q t )
|
In[17]:=
|
Factor[Kh[T87, Modulus -> 11][q, t] - kh]
|
Out[17]=
|
0
|
JavaKh also works over the integers:
| ||||
For example, the 22nd homology group over of the torus knot T(8,7) at degree 73 is the 280 element torsion group :
In[19]:=
|
Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]
|
Out[19]=
|
ZMod[2, 4, 5, 7]
|
T(8,7) is currently not on the Knot Atlas. Let us see what it looks like:
In[20]:=
|
Show[TubePlot[TorusKnot[8, 7]]]
|
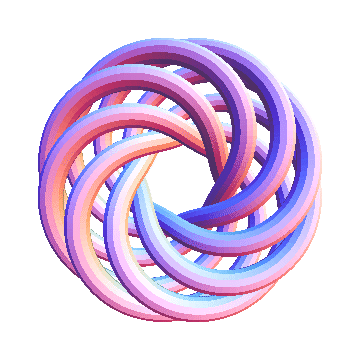
| |
Out[20]=
|
-Graphics3D-
|
Finally, JavaKh may also be run outside of Mathematica, as the following example demonstrates:
drorbn@coxeter:.../KnotTheory: cd JavaKh drorbn@coxeter:.../KnotTheory/JavaKh: java JavaKh PD[X[3, 1, 4, 6], X[1, 5, 2, 4], X[5, 3, 6, 2]] "+ q^1t^0 + q^3t^0 + q^5t^2 + q^9t^3 "
(Type java JavaKh -help for some further help).
(Warning, as of August 2008, you need to include the .jar files in JavaKh/jars on the classpath. If this causes confusion, ask Scott for a script that manages this automatically, or look at p. 29 of [1] for an example.)
Universal Khovanov homology, and reduced homology
The KnotTheory` package can now compute the universal homology over , the reduced homology over as well as directly computing the s-invariant. Type ?UniversalKh, ?KhReduced or ?sInvariant for more information.
The output of UniversalKh is a -linear combination of symbols KhE and KhC[n] for some positive integer .
The coefficients of these symbols are individually knot invariants, capturing all of the information in the spectral sequences (over ) for both unreduced and reduced homology.
The s-invariant can be extracted from the output of UniversalKh: the coefficient of KhE is exactly .
The usual 2-variable Khovanov polynomial Kh[K][q,t] can be recovered from UniversalKh[K][q,t] by using the substitution rules
{KhE->q+q^-1,KhC[1]->t^-1 q^-3+ q^1,KhC[n_]/;n>=2:>(q+q^-1)(t^-1 q^(-2n)+1)};
and similarly the reduced Khovanov polynomial KhReduced[K][q,t] is actually produced by substituting UniversalKh[K][q,t] using the rules
{KhE->q^-1,KhC[n_]:>t^-1 q^(-2n-1)+q^-1};
Unfortunately, much of the mathematics behind UniversalKh is not in print. There's some explanation in Scott's slides from Kyoto.
UniversalKh also takes the same JavaOptions option described above for Kh, which may be necessary to allow enough memory for large computations.
References
[Bar-Natan1] ^ D. Bar-Natan, On Khovanov's categorification of the Jones polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370, arXiv:math.GT/0201043.
[Bar-Natan2] ^ D. Bar-Natan, Khovanov's Homology for Tangles and Cobordisms, Geometry and Topology 9-33 (2005) 1443-1499, arXiv:math.GT/0410495.
[Bar-Natan3] ^ D. Bar-Natan, I've Computed Kh(T(9,5)) and I'm Happy, talk given at Knots in Washington XX, George Washington University, February 2005.
[Khovanov1] ^ M. Khovanov, A categorification of the Jones polynomial, arXiv:math.QA/9908171.
[Khovanov2] ^ M. Khovanov, An invariant of tangle cobordisms, arXiv:math.QA/0207264.
See also A Khovanov homology bibliography.















![{\displaystyle \mathbb {N} [q,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acbaffd1db67f47e1ca5f6c63bed36cff66b7673)

