L10n43

L10n42

L10n44

(Knotscape image)	See the full Thistlethwaite Link Table (up to 11 crossings). Visit L10n43 at Knotilus!

Link Presentations

[edit Notes on L10n43's Link Presentations]

Planar diagram presentation	X8192 X10,4,11,3 X20,10,7,9 X2738 X4,15,5,16 X5,13,6,12 X16,12,17,11 X17,6,18,1 X19,15,20,14 X13,19,14,18
Gauss code	{1, -4, 2, -5, -6, 8}, {4, -1, 3, -2, 7, 6, -10, 9, 5, -7, -8, 10, -9, -3}

A Braid Representative
A Morse Link Presentation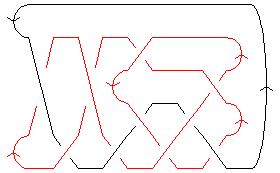

Polynomial invariants

Multivariable Alexander Polynomial (in $u$, $v$, $w$, ...)	$\frac{u^2 v^2-2 u^2 v+u^2-3 u v^2+5 u v-3 u+v^2-2 v+1}{u v}$ (db)
Jones polynomial	$-q^{13/2}+3 q^{11/2}-4 q^{9/2}+6 q^{7/2}-7 q^{5/2}+6 q^{3/2}-6 \sqrt{q}+\frac{3}{\sqrt{q}}-\frac{2}{q^{3/2}}$ (db)
Signature	1 (db)
HOMFLY-PT polynomial	$z^5 a^{-3} -3 z^3 a^{-1} +3 z^3 a^{-3} -z^3 a^{-5} +2 a z-6 z a^{-1} +4 z a^{-3} -z a^{-5} +2 a z^{-1} -3 a^{-1} z^{-1} + a^{-3} z^{-1}$ (db)
Kauffman polynomial	$z^5 a^{-7} -2 z^3 a^{-7} +3 z^6 a^{-6} -8 z^4 a^{-6} +4 z^2 a^{-6} +3 z^7 a^{-5} -7 z^5 a^{-5} +4 z^3 a^{-5} -2 z a^{-5} +z^8 a^{-4} +3 z^6 a^{-4} -12 z^4 a^{-4} +9 z^2 a^{-4} - a^{-4} +5 z^7 a^{-3} -13 z^5 a^{-3} +15 z^3 a^{-3} -7 z a^{-3} + a^{-3} z^{-1} +z^8 a^{-2} +z^6 a^{-2} -4 z^4 a^{-2} +7 z^2 a^{-2} -3 a^{-2} +2 z^7 a^{-1} -5 z^5 a^{-1} +3 a z^3+12 z^3 a^{-1} -5 a z-10 z a^{-1} +2 a z^{-1} +3 a^{-1} z^{-1} +z^6+2 z^2-3$ (db)

Khovanov Homology

The coefficients of the monomials $t^rq^j$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$).

\   r    \    j   \ -2 -1 0 1 2 3 4 5 6 χ 14                 1 1 12               2   -2 10             2 1   1 8           4 2     -2 6         3 2       1 4       3 4         1 2     3 3           0 0   1 4             3 -2 1 2               -1 -4 2                 2

Integral Khovanov Homology (db, data source)

$\dim{\mathcal G}_{2r+i}\operatorname{KH}^r_{\mathbb Z}$ $i=0$ $i=2$ $r=-2$ ${\mathbb Z}^{2}$ ${\mathbb Z}$ $r=-1$ ${\mathbb Z}^{2}\oplus{\mathbb Z}_2$ ${\mathbb Z}$ $r=0$ ${\mathbb Z}^{4}\oplus{\mathbb Z}_2^{2}$ ${\mathbb Z}^{3}$ $r=1$ ${\mathbb Z}^{3}\oplus{\mathbb Z}_2^{3}$ ${\mathbb Z}^{3}$ $r=2$ ${\mathbb Z}^{4}\oplus{\mathbb Z}_2^{3}$ ${\mathbb Z}^{3}$ $r=3$ ${\mathbb Z}^{2}\oplus{\mathbb Z}_2^{4}$ ${\mathbb Z}^{4}$ $r=4$ ${\mathbb Z}^{2}\oplus{\mathbb Z}_2^{2}$ ${\mathbb Z}^{2}$ $r=5$ ${\mathbb Z}\oplus{\mathbb Z}_2^{2}$ ${\mathbb Z}^{2}$ $r=6$ ${\mathbb Z}_2$ ${\mathbb Z}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L10n42 L10n44