Invariants from Braid Theory: Difference between revisions
No edit summary |
DrorsRobot (talk | contribs) No edit summary |
||
| Line 6: | Line 6: | ||
<!--$$?BraidLength$$--> |
<!--$$?BraidLength$$--> |
||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{Help1|n=2|s=BraidLength}} |
|||
BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`. |
|||
{{Help2}} |
|||
<!--END--> |
<!--END--> |
||
| Line 11: | Line 15: | ||
<!--$$K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}$$--> |
<!--$$K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}$$--> |
||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n=3}} |
|||
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]} |
|||
{{InOut2|n=3}}<pre style="border: 0px; padding: 0em"><nowiki>{11, 11}</nowiki></pre> |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
| Line 16: | Line 25: | ||
<!--$$?BraidIndex$$--> |
<!--$$?BraidIndex$$--> |
||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{HelpAndAbout1|n=4|s=BraidIndex}} |
|||
BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`. |
|||
{{HelpAndAbout2|n=5|s=BraidIndex}} |
|||
The braid index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/. |
|||
{{HelpAndAbout3}} |
|||
<!--END--> |
<!--END--> |
||
| Line 21: | Line 36: | ||
<!--$$K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}$$--> |
<!--$$K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}$$--> |
||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n=6}} |
|||
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]} |
|||
{{InOut2|n=6}}<pre style="border: 0px; padding: 0em"><nowiki>{4, 5}</nowiki></pre> |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$Show[BraidPlot[BR[K]]]$$--> |
<!--$$Show[BraidPlot[BR[K]]]$$--> |
||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{Graphics1|n=7}} |
|||
Show[BraidPlot[BR[K]]] |
|||
{{Graphics2|n=7|imagename=Invariants_from_Braid_Theory_Out_7.gif}} |
|||
<!--END--> |
<!--END--> |
||
Revision as of 21:02, 24 August 2005
The ``braid length`` of a knot or a link is the smallest number of crossings in a braid whose closure is . KnotTheory` has some braid lengths preloaded:
(For In[1] see Setup)
In[2]:= ?BraidLength
BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`. |
Note that the braid length of is simply the length of the minimum braid representing (see Braid Representatives):
| In[3]:= |
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]} |
| Out[3]= | {11, 11}
|
The ``braid index`` of a knot or a link is the smallest number of strands in a braid whose closure is . KnotTheory` has some braid indices preloaded:
In[4]:= ?BraidIndex
BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`. |
In[5]:= BraidIndex::about
The braid index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/. |
Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:
| In[6]:= |
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]} |
| Out[6]= | {4, 5}
|
| In[7]:= |
Show[BraidPlot[BR[K]]] |
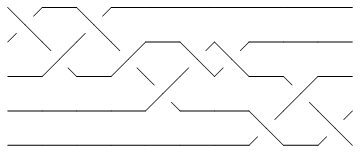
| |
| Out[7]= | -Graphics- |
