Heegaard Floer Knot Homology

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

In 2007, Jean-Marie Droz of the University of Zurich (working along with Anna Beliakova) wrote a Python program to compute the (hat-version) Heegaard-Floer Knot Homology ${\widehat {\operatorname {HFK} }}(K)$ of a knot $K$. His program is integrated into KnotTheory`, though to run it, you must have Python as well as the Python library Psycho installed on your system.

(For In[1] see Setup)

In[1]:= ?HFKHat HFKHat[K][t,m] returns the Poincare polynomial of the Heegaard-Floer Knot Homology (hat version) of the knot K, in the Alexander variable t and the Maslov variable m.

In[2]:= HFKHat::about The Heegaard-Floer Knot Homology program was written by Jean-Marie Droz in 2007 at the University of Zurich, based on methods of Anna Beliakova's arXiv:07050669.

8_19	in Arc Presentation

The Heegaard-Floer Knot Homology is a categorification of the Alexander polynomial. Let us test that for the knot 8_19:

In[3]:=	hfk = HFKHat[K = Knot[8, 19]][t, m]
Out[3]=	2 -3 m 5 2 6 3 m + t + -- + m t + m t 2 t

In[4]:=	{hfk /. m -> -1, Alexander[K][t]}
Out[4]=	-3 -2 2 3 -3 -2 2 3 {1 + t - t - t + t , 1 + t - t - t + t }

The knot 8_19 is the first knot in the Rolfsen Knot Table whose Heegaard-Floer Knot Homology is not "diagonal". Let us test that. The homology ${\widehat {\operatorname {HFK} }}(K)$ is "on diagonal", iff its Poincare polynomial, evaluated at $m=1/t$, is a monomial:

In[5]:=	Select[AllKnots[{3, 8}], (Head[HFKHat[#][t, 1/t]] == Plus) &]
Out[5]=	{Knot[8, 19]}

In[6]:=	hfk /. m -> 1/t
Out[6]=	4 -2 -- + t 3 t

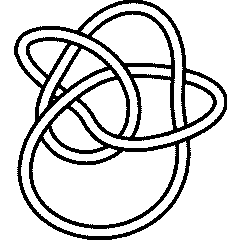
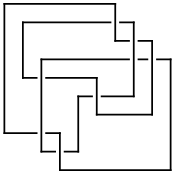
K11n34

K11n42

The Conway knot K11n34 and the Kinoshita-Terasaka knot K11n42 are a mutant pair, and are notoriously difficult to tell apart. Let us check that an array of standard knot polynomials fails to separate them, yet ${\widehat {\operatorname {HFK} }}$ succeeds:

In[7]:=	K1 = Knot["K11n34"]; K2 = Knot["K11n42"]; test[invt_] := (invt[K1] =!= invt[K2]); test /@ {Alexander, MultivariableAlexander, Jones, HOMFLYPT, Kauffman, Kh, HFKHat}
Out[7]=	{False, False, False, False, False, False, True}

Indeed,

In[8]:=	{HFKHat[K1][t, m], HFKHat[K2][t, m]}
Out[8]=	2 1 1 3 3 3 3 {3 + - + ----- + ----- + ----- + ----- + ---- + --- + 3 t + 3 m t + m 4 3 3 3 3 2 2 2 2 m t m t m t m t m t m t 2 2 2 2 3 3 3 3 m t + 3 m t + m t + m t , 6 1 1 4 4 2 2 2 7 + - + ----- + ----- + ---- + --- + 4 t + 4 m t + m t + m t } m 3 2 2 2 2 m t m t m t m t