R-Matrix Invariants: Difference between revisions
No edit summary |
m (Reverted edits by RacroCdelt (Talk); changed back to last version by Scott) |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 16: | Line 16: | ||
In more detail, let <math>V</math> be a free module of finite rank over a commutative ring, and let <math> R, \bar{R} \in End(V \otimes V) </math> be invertible. Further, let there be invertible endomorphisms <math>M_\leftarrow, M_\rightarrow, M^\leftarrow, M^\rightarrow \in End(V) </math>; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices. |
In more detail, let <math>V</math> be a free module of finite rank over a commutative ring, and let <math> R, \bar{R} \in End(V \otimes V) </math> be invertible. Further, let there be invertible endomorphisms <math>M_\leftarrow, M_\rightarrow, M^\leftarrow, M^\rightarrow \in End(V) </math>; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices. |
||
The following notation is useful: for <math>n = dim(V)</math>, <math>R_{ab}^{cd}</math> refers to the element of '''''R''''' in row <math>n(c-1)+d</math> |
The following notation is useful: for <math>n = dim(V)</math>, <math>R_{ab}^{cd}</math> refers to the element of '''''R''''' in row <math>n(c-1)+d</math> and column <math>n(a-1) + b</math>. |
||
For an oriented knot or link <math>K</math>, REngine returns the product <math> \tau(K) </math>, which is computed as follows: |
For an oriented knot or link <math>K</math>, REngine returns the product <math> \tau(K) </math>, which is computed as follows: |
||
| Line 46: | Line 46: | ||
:<math>M^\leftarrow = M^\rightarrow = M_\leftarrow = M_\rightarrow = \begin{pmatrix} 0&t^{-1/4} \\ t^{1/4}&0 \end{pmatrix} </math> |
:<math>M^\leftarrow = M^\rightarrow = M_\leftarrow = M_\rightarrow = \begin{pmatrix} 0&t^{-1/4} \\ t^{1/4}&0 \end{pmatrix} </math> |
||
Putting these definitions into Mathematica, we run the REngine on the [[3_1|trefoil]]. Note that the Jones polynomial is usually normalized so that the |
Putting these definitions into Mathematica, we run the REngine on the [[3_1|trefoil]]. Note that the Jones polynomial is usually normalized so that the polynomial of the unknot [[0_1]] is 1, hence the term on the denominator. |
||
<!--$$r={{Sqrt[t], 0, 0, 0},{0, 0, t, 0},{0,t, Sqrt[t] - t^(3/2), 0}, {0,0,0,Sqrt[t]}}; |
<!--$$r={{Sqrt[t], 0, 0, 0},{0, 0, t, 0},{0,t, Sqrt[t] - t^(3/2), 0}, {0,0,0,Sqrt[t]}}; |
||
rb = Inverse[r]; mcupl=mcapl=mcupr=mcapr={{0, t^(-1/4)},{t^(1/4), 0}};$$--> |
rb = Inverse[r]; mcupl=mcapl=mcupr=mcapr={{0, t^(-1/4)},{t^(1/4), 0}};$$--> |
||
| Line 60: | Line 60: | ||
{{InOut| |
{{InOut| |
||
n = 4 | |
n = 4 | |
||
in = <nowiki>jones = REngine[Knot[3,1], r, rb, mcupl, mcapl, mcupr, mcapr] |
in = <nowiki>jones = REngine[Knot[3,1], r, rb, mcupl, mcapl, mcupr, mcapr] / REngine[Knot[0,1], r, rb, mcupl, mcapr, mcupr, mcapr] //Apart</nowiki> | |
||
| ⚫ | |||
/ REngine[Knot[0,1], r, rb, mcupl, mcapr, mcupr, mcapr]</nowiki> | |
|||
-t + t + - |
|||
| ⚫ | |||
t</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
===See also=== |
|||
See also [[QuantumGroups`]], a Mathematica package by Scott Morrison, now included in KnotTheory`, which computes arbitrary quantum knot invariants. (For now, it only uses braid representations, not morse link representations.) |
|||
Latest revision as of 22:17, 27 May 2009
KnotTheory` can compute knot and link invariants associated with matrix solutions of the Yang-Baxter equation, using the program REngine:
(For In[1] see Setup)
|
| ||||||||
In more detail, let be a free module of finite rank over a commutative ring, and let be invertible. Further, let there be invertible endomorphisms ; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices.
The following notation is useful: for , refers to the element of R in row and column .
For an oriented knot or link , REngine returns the product , which is computed as follows:
- Find a Morse link presentation of such that it is composed only of crossings of the
X[k, Over/Under, Down, Down]variety; this is accomplished by adding caps and cups where necessary. - Label the edges in between events in the Morse link presentation of .
- Associate each event with one of the matrices as shown, with the indices given by the labelling:
- Define as the result of taking the product of the matrices associated with the elements of K, and summing over repeated indices; each sum runs from 1 to .
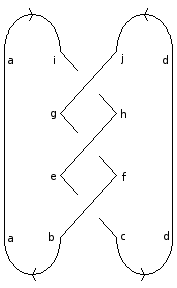
As an example, let K be the trefoil as shown, with the chosen axis upwards, and the strands going down through all the crossings. Then
where the summation is carried out on all the indices a through i, each ranging from 1 to n.
Determining that is actually an invariant is simply a matter of checking the equality of the outcomes of Reidemeister moves in various configurations and orientations, as well as a few 'topological' moves. Note that REngine does not perform any checks, while the utility TestRMatrix performs the tests required to determine regular isotopy.
Let's use the REngine to find the Jones polynomial of the trefoil. The R and M matrices for the Jones polynomial, in the indeterminate t, are as follows:
Putting these definitions into Mathematica, we run the REngine on the trefoil. Note that the Jones polynomial is usually normalized so that the polynomial of the unknot 0_1 is 1, hence the term on the denominator.
In[3]:=
|
r={{Sqrt[t], 0, 0, 0},{0, 0, t, 0},{0,t, Sqrt[t] - t^(3/2), 0}, {0,0,0,Sqrt[t]}};
rb = Inverse[r]; mcupl=mcapl=mcupr=mcapr={{0, t^(-1/4)},{t^(1/4), 0}};
|
In[4]:=
|
jones = REngine[Knot[3,1], r, rb, mcupl, mcapl, mcupr, mcapr] / REngine[Knot[0,1], r, rb, mcupl, mcapr, mcupr, mcapr] //Apart
|
Out[4]=
|
-4 -3 1
-t + t + -
t
|
See also
See also QuantumGroups`, a Mathematica package by Scott Morrison, now included in KnotTheory`, which computes arbitrary quantum knot invariants. (For now, it only uses braid representations, not morse link representations.)