Gauss Codes: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
The Gauss Code of an <math>n</math>-crossing knot or link <math>L</math> is obtained as follows: |
The Gauss Code of an <math>n</math>-crossing knot or link <math>L</math> is obtained as follows: |
||
* Number the crossings of |
* Number the crossings of <math>L</math> from 1 to <math>n</math> in an arbitrary manner. |
||
* Order the components of |
* Order the components of <math>L</math> is some arbitrary manner. |
||
* Start |
* Start "walking" along the first component of <math>L</math>, taking note of the numbers of the crossings you've gone through. If in a given crossing you cross on the "over" strand, write down the number of that crossing. If you cross on the "under" strand, write down the negative of the number of that crossing. |
||
* Do the same for all other components of |
* Do the same for all other components of <math>L</math> (if any). |
||
The resulting list of signed integers (in the case of a knot) or list of lists of signed integers (in the case of a link) is called the Gauss Code of <math>L</math>. <code>KnotTheory`</code> has some rudimentary support for Gauss codes: |
The resulting list of signed integers (in the case of a knot) or list of lists of signed integers (in the case of a link) is called the Gauss Code of <math>L</math>. <code>KnotTheory`</code> has some rudimentary support for Gauss codes: |
||
{{Startup Note}} |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
(For <tt><font color=blue>In[1]</font></tt> see [[Setup]]) |
|||
| ⚫ | |||
<!--$$?GaussCode$$--> |
<!--$$?GaussCode$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{HelpLine| |
|||
{| width=70% border=1 align=center |
|||
n = 2 | |
|||
| |
|||
in = <nowiki>GaussCode</nowiki> | |
|||
<font color=blue><tt>In[2]:=</tt></font><font color=red><code> ?GaussCode</code></font> |
|||
out= <nowiki>GaussCode[i1, i2, ...] represents a knot via its Gauss Code following the conventions used by the knotilus website, |
|||
http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/html/start.html. |
|||
| ⚫ | |||
| ⚫ | |||
Thus for example, the Gauss codes for the [[3_1|trefoil knot]] and the [[L6a4|Borromean link]] are: |
|||
<!--$$GaussCode /@ {Knot[3, 1], Link[6, Alternating, 4]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 3 | |
|||
in = <nowiki>GaussCode /@ {Knot[3, 1], Link[6, Alternating, 4]}</nowiki> | |
|||
out= <nowiki>{GaussCode[-1, 3, -2, 1, -3, 2], |
|||
GaussCode[{1, -6, 5, -3}, {4, -1, 2, -5}, {6, -4, 3, -2}]}</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Pair|3_1|gif|L6a4|gif}} |
|||
Ralph Furmaniak, working under the guidance of Stuart Rankin and Ortho Flint at the University of Western Ontario, wrote a web-based server called "Knotilus" that takes Gauss codes and outputs pictures of the desired knots and links in several standard image formats. |
|||
<!--$$?KnotilusURL$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 4 | |
|||
in = <nowiki>KnotilusURL</nowiki> | |
|||
out= <nowiki>KnotilusURL[K_] returns the URL of the knot/link K on the knotilus website, |
|||
http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/html/start.html.</nowiki>}} |
|||
<!--END--> |
|||
Thus, |
|||
<!--$$KnotilusURL /@ {Knot[3, 1], Link[6, Alternating, 4]}$$--> |
|||
| ⚫ | |||
<!--Robot Land, no human edits to "END"--> |
|||
|} |
|||
{{InOut| |
|||
n = 5 | |
|||
in = <nowiki>KnotilusURL /@ {Knot[3, 1], Link[6, Alternating, 4]}</nowiki> | |
|||
out= <nowiki>{http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/-1,3,-2,1,-3,2/goTop.h\ |
|||
tml, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-6,5,-3:4,-1,\ |
|||
2,-5:6,-4,3,-2/goTop.html}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
Latest revision as of 17:09, 21 February 2013
The Gauss Code of an -crossing knot or link is obtained as follows:
- Number the crossings of from 1 to in an arbitrary manner.
- Order the components of is some arbitrary manner.
- Start "walking" along the first component of , taking note of the numbers of the crossings you've gone through. If in a given crossing you cross on the "over" strand, write down the number of that crossing. If you cross on the "under" strand, write down the negative of the number of that crossing.
- Do the same for all other components of (if any).
The resulting list of signed integers (in the case of a knot) or list of lists of signed integers (in the case of a link) is called the Gauss Code of . KnotTheory` has some rudimentary support for Gauss codes:
(For In[1] see Setup)
| ||||
Thus for example, the Gauss codes for the trefoil knot and the Borromean link are:
In[3]:=
|
GaussCode /@ {Knot[3, 1], Link[6, Alternating, 4]}
|
Out[3]=
|
{GaussCode[-1, 3, -2, 1, -3, 2],
GaussCode[{1, -6, 5, -3}, {4, -1, 2, -5}, {6, -4, 3, -2}]}
|
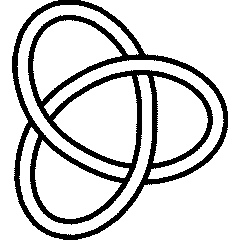 3_1 |
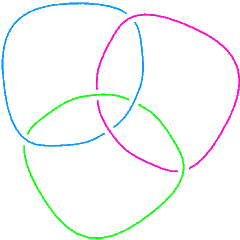 L6a4 |
Ralph Furmaniak, working under the guidance of Stuart Rankin and Ortho Flint at the University of Western Ontario, wrote a web-based server called "Knotilus" that takes Gauss codes and outputs pictures of the desired knots and links in several standard image formats.
| ||||
Thus,
In[5]:=
|
KnotilusURL /@ {Knot[3, 1], Link[6, Alternating, 4]}
|
Out[5]=
|
{http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/-1,3,-2,1,-3,2/goTop.h\
tml, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-6,5,-3:4,-1,\
2,-5:6,-4,3,-2/goTop.html}
|

