Invariants from Braid Theory: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
m (Reverted edits by VitrrAccna (Talk); changed back to last version by Scott) |
No edit summary |
||
| Line 8: | Line 8: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 2 | |
||
in = <nowiki>BraidLength</nowiki> | |
in = <nowiki>BraidLength</nowiki> | |
||
out= <nowiki>BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`.</nowiki>}} |
out= <nowiki>BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`.</nowiki>}} |
||
| Line 18: | Line 18: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 3 | |
||
in = <nowiki>K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}</nowiki> | |
in = <nowiki>K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}</nowiki> | |
||
out= <nowiki>{11, 11}</nowiki>}} |
out= <nowiki>{11, 11}</nowiki>}} |
||
| Line 30: | Line 30: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpAndAbout| |
{{HelpAndAbout| |
||
n = |
n = 4 | |
||
n1 = |
n1 = 5 | |
||
in = <nowiki>BraidIndex</nowiki> | |
in = <nowiki>BraidIndex</nowiki> | |
||
out= <nowiki>BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`.</nowiki> | |
out= <nowiki>BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`.</nowiki> | |
||
| Line 42: | Line 42: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 6 | |
||
in = <nowiki>K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}</nowiki> | |
in = <nowiki>K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}</nowiki> | |
||
out= <nowiki>{4, 5}</nowiki>}} |
out= <nowiki>{4, 5}</nowiki>}} |
||
| Line 52: | Line 52: | ||
n = 7 | |
n = 7 | |
||
in = <nowiki>Show[BraidPlot[BR[K]]]</nowiki> | |
in = <nowiki>Show[BraidPlot[BR[K]]]</nowiki> | |
||
img= |
img= Invariants_from_Braid_Theory_Out_7.gif | |
||
out= <nowiki>-Graphics-</nowiki>}} |
out= <nowiki>-Graphics-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
Latest revision as of 17:20, 21 February 2013
The braid length of a knot or a link is the smallest number of crossings in a braid whose closure is . KnotTheory` has some braid lengths preloaded:
(For In[1] see Setup)
| ||||
Note that the braid length of is simply the length of the minimum braid representing (see Braid Representatives):
In[3]:=
|
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}
|
Out[3]=
|
{11, 11}
|
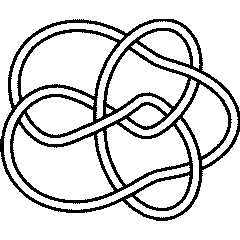 9_49 |
 10_136 |
The braid index of a knot or a link is the smallest number of strands in a braid whose closure is . KnotTheory` has some braid indices preloaded:
|
| ||||||||
Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:
In[6]:=
|
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}
|
Out[6]=
|
{4, 5}
|
In[7]:=
|
Show[BraidPlot[BR[K]]]
|
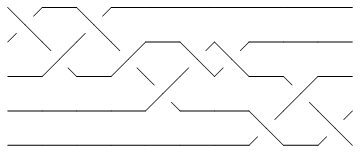
| |
Out[7]=
|
-Graphics-
|
