Khovanov Homology: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| (23 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
(See also: [[Tweaking JavaKh]]) |
|||
| ⚫ | The Khovanov Homology <math>\operatorname{\it KH}(L)</math> of a knot or a link <math>L</math>, also known as Khovanov's categorification of the Jones polynomial of <math>L</math>, was defined by Khovanov in {{ref|Khovanov1}} (also check {{ref|Bar-Natan1}}), where the notation is closer to the notation used here). It is a graded homology theory; each homology group <math>\operatorname{\it KH}^r(L)</math> is in itself a direct sum <math>\bigoplus_j\operatorname{\it KH}^r_j(L)</math> of homogeneous components. Over a field |
||
| ⚫ | The Khovanov Homology <math>\operatorname{\it KH}(L)</math> of a knot or a link <math>L</math>, also known as Khovanov's categorification of the Jones polynomial of <math>L</math>, was defined by Khovanov in {{ref|Khovanov1}} (also check {{ref|Bar-Natan1}}), where the notation is closer to the notation used here). It is a graded homology theory; each homology group <math>\operatorname{\it KH}^r(L)</math> is in itself a direct sum <math>\bigoplus_j\operatorname{\it KH}^r_j(L)</math> of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" <math>\operatorname{\it Kh}(L)</math> (which deserves the name "the Khovanov polynomial of <math>L</math>"), |
||
<center><math>\operatorname{\it Kh}(L)(q,t) := \sum_{r,j}t^rq^j\dim\operatorname{\it KH}^r_j(L)</math>.</center> |
<center><math>\operatorname{\it Kh}(L)(q,t) := \sum_{r,j}t^rq^j\dim\operatorname{\it KH}^r_j(L)</math>.</center> |
||
| Line 10: | Line 12: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 2 | |
||
in = <nowiki>Kh</nowiki> | |
in = <nowiki>Kh</nowiki> | |
||
out= <nowiki>Kh[L][q, t] returns the Poincare polynomial of the Khovanov Homology of a knot/link L (over a field of characteristic 0) in terms of the variables q and t. Kh[L, Program -> prog] uses the |
out= <nowiki>Kh[L][q, t] returns the Poincare polynomial of the Khovanov Homology of a knot/link L (over a field of characteristic 0) in terms of the variables q and t. Kh[L, Program -> prog] uses the |
||
program prog to perform the computation. The currently available programs are "FastKh", written in Mathematica by Dror Bar-Natan in the winter of 2005, "JavaKh-v1", written in java (java 1.5 |
|||
required!) by Jeremy Green in the summer of 2005 and "JavaKh-v2" (default), an update of "JavaKh-v1" (now requiring java 1.6) written by Scott Morrison in 2008. |
|||
("JavaKh" is also available, currently an alias for "JavaKh-v2".) |
|||
The java programs are several thousand times faster than the Mathematica program, though java may not be available on some systems. "JavaKh2" also takes the option "Modulus -> p" which changes the characteristic of the ground field to p. If p==0 JavaKh works over the rational numbers; if p==Null JavaKh works over Z (see ?ZMod for the output format).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
| Line 20: | Line 26: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 3 | |
||
in = <nowiki>kh = Kh[Knot[5, 1]][q, t]</nowiki> | |
in = <nowiki>kh = Kh[Knot[5, 1]][q, t]</nowiki> | |
||
out= <nowiki> -5 -3 1 1 1 1 |
out= <nowiki> -5 -3 1 1 1 1 |
||
| Line 37: | Line 43: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 4 | |
||
in = <nowiki>{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}</nowiki> | |
in = <nowiki>{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}</nowiki> | |
||
out= <nowiki> -15 -7 -5 -3 -15 -7 -5 -3 |
out= <nowiki> -15 -7 -5 -3 -15 -7 -5 -3 |
||
{-q + q + q + q , -q + q + q + q }</nowiki>}} |
{-q + q + q + q , -q + q + q + q }</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
{{Knot Image Pair|5_1|gif|10_132|gif}} |
|||
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, <math>J(5_1)=J(10_{132})</math> though <math>\operatorname{\it Kh}(5_1)\neq\operatorname{\it Kh}(10_{132})</math>: |
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, <math>J(5_1)=J(10_{132})</math> though <math>\operatorname{\it Kh}(5_1)\neq\operatorname{\it Kh}(10_{132})</math>: |
||
| Line 51: | Line 59: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 5 | |
||
in = <nowiki>{ |
in = <nowiki>{ |
||
Jones[Knot[5, 1]] === Jones[Knot[10, 132]], |
Jones[Knot[5, 1]] === Jones[Knot[10, 132]], |
||
| Line 62: | Line 70: | ||
* <tt>FastKh</tt>: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax <code>Kh[L, Program -> "FastKh"][q, t]</code> or by changing the default behaviour of <code>Kh</code> by evaluating <code>SetOptions[Kh, Program -> "FastKh"]</code>. |
* <tt>FastKh</tt>: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax <code>Kh[L, Program -> "FastKh"][q, t]</code> or by changing the default behaviour of <code>Kh</code> by evaluating <code>SetOptions[Kh, Program -> "FastKh"]</code>. |
||
* <tt>JavaKh</tt>: In the summer of 2005 Jeremy Green re-implemented the algorithm in java ''' |
* <tt>JavaKh</tt>: In the summer of 2005 Jeremy Green re-implemented the algorithm in java ('''java 1.5 required''', can be had from http://java.sun.com/) with much further care to the details, leading to an improvement factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax <code>Kh[L, Program -> "JavaKh"][q, t]</code>. |
||
<!--$$Options[Kh]$$--> |
<!--$$Options[Kh]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 6 | |
||
in = <nowiki>Options[Kh]</nowiki> | |
in = <nowiki>Options[Kh]</nowiki> | |
||
out= <nowiki>{ExpansionOrder -> Automatic, Program -> JavaKh, Modulus -> 0, |
out= <nowiki>{ExpansionOrder -> Automatic, Program -> JavaKh-v2, Modulus -> 0, |
||
JavaOptions -> }</nowiki>}} |
KnotTheory`FastKh`Universal -> False, JavaOptions -> }</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 79: | Line 87: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{In| |
{{In| |
||
n = |
n = 7 | |
||
in = <nowiki>T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];</nowiki>}} |
in = <nowiki>T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 92: | Line 100: | ||
Kh[TorusKnot[6, 5], Modulus->7] = Function @@ {kh /. {q->#1, t->#2}}; |
Kh[TorusKnot[6, 5], Modulus->7] = Function @@ {kh /. {q->#1, t->#2}}; |
||
$--><!--END--> |
$--><!--END--> |
||
<!--$$Kh[T65, Modulus -> 3][q, t] - kh$$--> |
<!--$$Kh[T65, Modulus -> 3][q, t] - kh$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 8 | |
||
in = <nowiki>Kh[T65, Modulus -> 3][q, t] - kh</nowiki> | |
in = <nowiki>Kh[T65, Modulus -> 3][q, t] - kh</nowiki> | |
||
out= <nowiki> 43 13 43 14 |
out= <nowiki> 43 13 43 14 |
||
| Line 105: | Line 112: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 9 | |
||
in = <nowiki>Kh[T65, Modulus -> 5][q, t] - kh</nowiki> | |
in = <nowiki>Kh[T65, Modulus -> 5][q, t] - kh</nowiki> | |
||
out= <nowiki> 35 10 35 11 39 11 39 12 |
out= <nowiki> 35 10 35 11 39 11 39 12 |
||
| Line 114: | Line 121: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 10 | |
||
in = <nowiki>Kh[T65, Modulus -> 7][q, t] - kh</nowiki> | |
in = <nowiki>Kh[T65, Modulus -> 7][q, t] - kh</nowiki> | |
||
out= <nowiki>0</nowiki>}} |
out= <nowiki>0</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
{{Knot Image|T(6,5)|jpg}} |
|||
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion: |
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion: |
||
| Line 124: | Line 133: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 11 | |
||
in = <nowiki>JavaOptions</nowiki> | |
in = <nowiki>JavaOptions</nowiki> | |
||
out= <nowiki>JavaOptions is an option to Kh. Kh[L, Program -> " |
out= <nowiki>JavaOptions is an option to Kh. Kh[L, Program -> "JavaKh2", JavaOptions -> jopts] calls java with options jopts. Thus for example, JavaOptions -> "-Xmx256m" sets the maximum java heap size to 256MB - useful for large computations.</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 132: | Line 141: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{In| |
{{In| |
||
n = |
n = 12 | |
||
in = <nowiki>SetOptions[Kh, JavaOptions -> "-Xmx256m"];</nowiki>}} |
in = <nowiki>SetOptions[Kh, JavaOptions -> "-Xmx256m"];</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 153: | Line 162: | ||
}; |
}; |
||
$--><!--END--> |
$--><!--END--> |
||
<!--$$T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];$$--> |
<!--$$T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{In| |
{{In| |
||
n = |
n = 13 | |
||
in = <nowiki>T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];</nowiki>}} |
in = <nowiki>T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 179: | Line 187: | ||
Kh[TorusKnot[8, 7], Modulus->11] = Function @@ {kh /. {q->#1, t->#2}}; |
Kh[TorusKnot[8, 7], Modulus->11] = Function @@ {kh /. {q->#1, t->#2}}; |
||
$--><!--END--> |
$--><!--END--> |
||
<!--$$Factor[Kh[T87, Modulus -> 3][q, t] - kh]$$--> |
<!--$$Factor[Kh[T87, Modulus -> 3][q, t] - kh]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 14 | |
||
in = <nowiki>Factor[Kh[T87, Modulus -> 3][q, t] - kh]</nowiki> | |
in = <nowiki>Factor[Kh[T87, Modulus -> 3][q, t] - kh]</nowiki> | |
||
out= <nowiki> 79 25 |
out= <nowiki> 79 25 |
||
| Line 192: | Line 199: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 15 | |
||
in = <nowiki>Factor[Kh[T87, Modulus -> 5][q, t] - kh]</nowiki> | |
in = <nowiki>Factor[Kh[T87, Modulus -> 5][q, t] - kh]</nowiki> | |
||
out= <nowiki> 61 11 12 10 14 12 18 13 |
out= <nowiki> 61 11 12 10 14 12 18 13 |
||
| Line 201: | Line 208: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 16 | |
||
in = <nowiki>Factor[Kh[T87, Modulus -> 7][q, t] - kh]</nowiki> | |
in = <nowiki>Factor[Kh[T87, Modulus -> 7][q, t] - kh]</nowiki> | |
||
out= <nowiki> 61 14 8 6 12 7 10 8 14 9 |
out= <nowiki> 61 14 8 6 12 7 10 8 14 9 |
||
| Line 210: | Line 217: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 17 | |
||
in = <nowiki>Factor[Kh[T87, Modulus -> 11][q, t] - kh]</nowiki> | |
in = <nowiki>Factor[Kh[T87, Modulus -> 11][q, t] - kh]</nowiki> | |
||
out= <nowiki>0</nowiki>}} |
out= <nowiki>0</nowiki>}} |
||
| Line 220: | Line 227: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 18 | |
||
in = <nowiki>ZMod</nowiki> | |
in = <nowiki>ZMod</nowiki> | |
||
out= <nowiki>ZMod[m] denotes the cyclic group Z/mZ. Thus if m=0 it is the infinite cyclic group Z and if m>0 it is the finite cyclic group with m elements. ZMod[m1, m2, ...] denotes the direct sum of ZMod[m1], ZMod[m2], ... .</nowiki>}} |
out= <nowiki>ZMod[m] denotes the cyclic group Z/mZ. Thus if m=0 it is the infinite cyclic group Z and if m>0 it is the finite cyclic group with m elements. ZMod[m1, m2, ...] denotes the direct sum of ZMod[m1], ZMod[m2], ... .</nowiki>}} |
||
| Line 235: | Line 242: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 19 | |
||
in = <nowiki>Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]</nowiki> | |
in = <nowiki>Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]</nowiki> | |
||
out= <nowiki>ZMod[2, 4, 5, 7]</nowiki>}} |
out= <nowiki>ZMod[2, 4, 5, 7]</nowiki>}} |
||
<!--END--> |
|||
T(8,7) is currently not on the Knot Atlas. Let us see what it looks like: |
|||
<!--$$Show[TubePlot[TorusKnot[8, 7]]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{Graphics| |
|||
n = 20 | |
|||
in = <nowiki>Show[TubePlot[TorusKnot[8, 7]]]</nowiki> | |
|||
img= Khovanov_Homology_Out_20.gif | |
|||
out= <nowiki>-Graphics3D-</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
| Line 249: | Line 267: | ||
(Type <tt>java JavaKh -help</tt> for some further help). |
(Type <tt>java JavaKh -help</tt> for some further help). |
||
('''Warning''', as of August 2008, you need to include the .jar files in JavaKh/jars on the classpath. If this causes confusion, ask Scott for a script that manages this automatically, or look at p. 29 of [http://arxiv.org/abs/0906.5177] for an example.) |
|||
| ⚫ | |||
===Universal Khovanov homology, and reduced homology=== |
|||
The KnotTheory` package can now compute the universal homology over <math>\mathbb{Q}</math>, the reduced homology over <math>\mathbb{Q}</math> as well as directly computing the s-invariant. Type <code>?UniversalKh</code>, <code>?KhReduced</code> or <code>?sInvariant</code> for more information. |
|||
The output of <code>UniversalKh</code> is a <math>\mathbb{N}[q,t]</math>-linear combination of symbols <code>KhE</code> and <code>KhC[n]</code> for some positive integer <math>n</math>. |
|||
The coefficients of these symbols are individually knot invariants, capturing all of the information in the spectral sequences (over <math>\mathbb{Q}</math>) for both unreduced and reduced homology. |
|||
The s-invariant can be extracted from the output of <code>UniversalKh</code>: the coefficient of KhE is exactly <math>q^s</math>. |
|||
The usual 2-variable Khovanov polynomial <code>Kh[K][q,t]</code> can be recovered from <code>UniversalKh[K][q,t]</code> by using the substitution rules |
|||
{KhE->q+q^-1,KhC[1]->t^-1 q^-3+ q^1,KhC[n_]/;n>=2:>(q+q^-1)(t^-1 q^(-2n)+1)}; |
|||
and similarly the reduced Khovanov polynomial <code>KhReduced[K][q,t]</code> is actually produced by substituting <code>UniversalKh[K][q,t]</code> using the rules |
|||
{KhE->q^-1,KhC[n_]:>t^-1 q^(-2n-1)+q^-1}; |
|||
Unfortunately, much of the mathematics behind <code>UniversalKh</code> is not in print. There's some explanation in [http://tqft.net/kyoto2 Scott's slides] from Kyoto. |
|||
UniversalKh also takes the same JavaOptions option described above for Kh, which may be necessary to allow enough memory for large computations. |
|||
===References=== |
|||
| ⚫ | |||
{{note|Bar-Natan1}} D. Bar-Natan, [http://www.math.toronto.edu/~drorbn/papers/Categorification/ ''On Khovanov's categorification of the Jones polynomial''], Algebraic and Geometric Topology '''2-16''' (2002) 337-370, {{arXiv|math.GT/0201043}}. |
{{note|Bar-Natan1}} D. Bar-Natan, [http://www.math.toronto.edu/~drorbn/papers/Categorification/ ''On Khovanov's categorification of the Jones polynomial''], Algebraic and Geometric Topology '''2-16''' (2002) 337-370, {{arXiv|math.GT/0201043}}. |
||
| Line 260: | Line 302: | ||
{{note|Khovanov2}} M. Khovanov, ''An invariant of tangle cobordisms'', {{arXiv|math.QA/0207264}}. |
{{note|Khovanov2}} M. Khovanov, ''An invariant of tangle cobordisms'', {{arXiv|math.QA/0207264}}. |
||
See also [[A Khovanov homology bibliography]]. |
|||
Latest revision as of 18:23, 21 February 2013
(See also: Tweaking JavaKh)
The Khovanov Homology of a knot or a link , also known as Khovanov's categorification of the Jones polynomial of , was defined by Khovanov in [Khovanov1] (also check [Bar-Natan1]), where the notation is closer to the notation used here). It is a graded homology theory; each homology group is in itself a direct sum of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" (which deserves the name "the Khovanov polynomial of "),
(For In[1] see Setup)
| ||||
Thus for example, here's the Khovanov polynomial of the knot 5_1:
In[3]:=
|
kh = Kh[Knot[5, 1]][q, t]
|
Out[3]=
|
-5 -3 1 1 1 1
q + q + ------ + ------ + ------ + -----
15 5 11 4 11 3 7 2
q t q t q t q t
|
The Euler characteristic of the Khovanov Homology is (up to normalization) the Jones polynomial of . Precisely,
Let us verify this in the case of 5_1:
In[4]:=
|
{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}
|
Out[4]=
|
-15 -7 -5 -3 -15 -7 -5 -3
{-q + q + q + q , -q + q + q + q }
|
 5_1 |
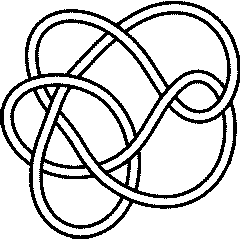 10_132 |
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, though :
In[5]:=
|
{
Jones[Knot[5, 1]] === Jones[Knot[10, 132]],
Kh[Knot[5, 1]] === Kh[Knot[10, 132]]
}
|
Out[5]=
|
{True, False}
|
The algorithm presently used by KnotTheory` is an efficient algorithm modeled on the Kauffman bracket algorithm of The Jones Polynomial, as explained in [Bar-Natan3] (which follows [Bar-Natan2]). Currently, two implementations of this algorithm are available:
- FastKh: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax
Kh[L, Program -> "FastKh"][q, t]or by changing the default behaviour ofKhby evaluatingSetOptions[Kh, Program -> "FastKh"]. - JavaKh: In the summer of 2005 Jeremy Green re-implemented the algorithm in java (java 1.5 required, can be had from http://java.sun.com/) with much further care to the details, leading to an improvement factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax
Kh[L, Program -> "JavaKh"][q, t].
In[6]:=
|
Options[Kh]
|
Out[6]=
|
{ExpansionOrder -> Automatic, Program -> JavaKh-v2, Modulus -> 0,
KnotTheory`FastKh`Universal -> False, JavaOptions -> }
|
JavaKh takes an additional option, Modulus, which sets the characteristic of the ground field for the homology computations to or to a prime . Thus for example, the following four In lines imply that the Khovanov homology of the torus knot T(6,5) has both 3 torsion and 5 torsion, but no 7 torsion:
In[7]:=
|
T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];
|
In[8]:=
|
Kh[T65, Modulus -> 3][q, t] - kh
|
Out[8]=
|
43 13 43 14
q t + q t
|
In[9]:=
|
Kh[T65, Modulus -> 5][q, t] - kh
|
Out[9]=
|
35 10 35 11 39 11 39 12
q t + q t + q t + q t
|
In[10]:=
|
Kh[T65, Modulus -> 7][q, t] - kh
|
Out[10]=
|
0
|
 T(6,5) |
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion:
| ||||
In[12]:=
|
SetOptions[Kh, JavaOptions -> "-Xmx256m"];
|
In[13]:=
|
T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];
|
In[14]:=
|
Factor[Kh[T87, Modulus -> 3][q, t] - kh]
|
Out[14]=
|
79 25
q t (1 + t)
|
In[15]:=
|
Factor[Kh[T87, Modulus -> 5][q, t] - kh]
|
Out[15]=
|
61 11 12 10 14 12 18 13
q t (1 + t) (1 + q t + q t + q t )
|
In[16]:=
|
Factor[Kh[T87, Modulus -> 7][q, t] - kh]
|
Out[16]=
|
61 14 8 6 12 7 10 8 14 9
q t (1 + t) (1 + q t + q t + q t + q t )
|
In[17]:=
|
Factor[Kh[T87, Modulus -> 11][q, t] - kh]
|
Out[17]=
|
0
|
JavaKh also works over the integers:
| ||||
For example, the 22nd homology group over of the torus knot T(8,7) at degree 73 is the 280 element torsion group :
In[19]:=
|
Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]
|
Out[19]=
|
ZMod[2, 4, 5, 7]
|
T(8,7) is currently not on the Knot Atlas. Let us see what it looks like:
In[20]:=
|
Show[TubePlot[TorusKnot[8, 7]]]
|
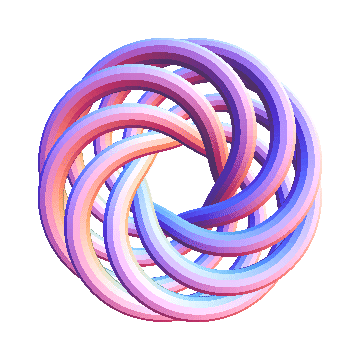
| |
Out[20]=
|
-Graphics3D-
|
Finally, JavaKh may also be run outside of Mathematica, as the following example demonstrates:
drorbn@coxeter:.../KnotTheory: cd JavaKh drorbn@coxeter:.../KnotTheory/JavaKh: java JavaKh PD[X[3, 1, 4, 6], X[1, 5, 2, 4], X[5, 3, 6, 2]] "+ q^1t^0 + q^3t^0 + q^5t^2 + q^9t^3 "
(Type java JavaKh -help for some further help).
(Warning, as of August 2008, you need to include the .jar files in JavaKh/jars on the classpath. If this causes confusion, ask Scott for a script that manages this automatically, or look at p. 29 of [1] for an example.)
Universal Khovanov homology, and reduced homology
The KnotTheory` package can now compute the universal homology over , the reduced homology over as well as directly computing the s-invariant. Type ?UniversalKh, ?KhReduced or ?sInvariant for more information.
The output of UniversalKh is a -linear combination of symbols KhE and KhC[n] for some positive integer .
The coefficients of these symbols are individually knot invariants, capturing all of the information in the spectral sequences (over ) for both unreduced and reduced homology.
The s-invariant can be extracted from the output of UniversalKh: the coefficient of KhE is exactly .
The usual 2-variable Khovanov polynomial Kh[K][q,t] can be recovered from UniversalKh[K][q,t] by using the substitution rules
{KhE->q+q^-1,KhC[1]->t^-1 q^-3+ q^1,KhC[n_]/;n>=2:>(q+q^-1)(t^-1 q^(-2n)+1)};
and similarly the reduced Khovanov polynomial KhReduced[K][q,t] is actually produced by substituting UniversalKh[K][q,t] using the rules
{KhE->q^-1,KhC[n_]:>t^-1 q^(-2n-1)+q^-1};
Unfortunately, much of the mathematics behind UniversalKh is not in print. There's some explanation in Scott's slides from Kyoto.
UniversalKh also takes the same JavaOptions option described above for Kh, which may be necessary to allow enough memory for large computations.
References
[Bar-Natan1] ^ D. Bar-Natan, On Khovanov's categorification of the Jones polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370, arXiv:math.GT/0201043.
[Bar-Natan2] ^ D. Bar-Natan, Khovanov's Homology for Tangles and Cobordisms, Geometry and Topology 9-33 (2005) 1443-1499, arXiv:math.GT/0410495.
[Bar-Natan3] ^ D. Bar-Natan, I've Computed Kh(T(9,5)) and I'm Happy, talk given at Knots in Washington XX, George Washington University, February 2005.
[Khovanov1] ^ M. Khovanov, A categorification of the Jones polynomial, arXiv:math.QA/9908171.
[Khovanov2] ^ M. Khovanov, An invariant of tangle cobordisms, arXiv:math.QA/0207264.
See also A Khovanov homology bibliography.















![{\displaystyle \mathbb {N} [q,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acbaffd1db67f47e1ca5f6c63bed36cff66b7673)

