Khovanov Homology

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

The Khovanov Homology $\operatorname {\it {KH}} (L)$ of a knot or a link $L$, also known as Khovanov's categorification of the Jones polynomial of $L$, was defined by Khovanov in [Khovanov1] (also check [Bar-Natan1]), where the notation is closer to the notation used here). It is a graded homology theory; each homology group $\operatorname {\it {KH}} ^{r}(L)$ is in itself a direct sum $\bigoplus _{j}\operatorname {\it {KH}} _{j}^{r}(L)$ of homogeneous components. Over a field on can form the two-variable "Poincar'e polynomial" $\operatorname {\it {Kh}} (L)$ (which deserves the name "the Khovanov polynomial of $L$"),

$\operatorname {\it {Kh}} (L)(q,t):=\sum _{r,j}t^{r}q^{j}\dim \operatorname {\it {KH}} _{j}^{r}(L)$.

(For In[1] see Setup)

In[2]:= ?Kh Kh[L][q, t] returns the Poincare polynomial of the Khovanov Homology of a knot/link L (over a field of characteristic 0) in terms of the variables q and t. Kh[L, Program -> prog] uses the program prog to perform the computation. The currently available programs are "FastKh", written in Mathematica by Dror Bar-Natan in the winter of 2005 and "JavaKh" (default), written in java (java 1.5 required!) by Jeremy Green in the summer of 2005. The java program is several thousand times faster than the Mathematica program, though java may not be available on some systems. "JavaKh" also takes the option "Modulus -> p" which changes the characteristic of the ground field to p. If p==0 JavaKh works over the rational numbers; if p==Null JavaKh works over Z (see ?ZMod for the output format).

Thus for example, here's the Khovanov polynomial of the knot 5_1:

In[3]:=	kh = Kh[Knot[5, 1]][q, t]
Out[3]=	-5 -3 1 1 1 1 q + q + ------ + ------ + ------ + ----- 15 5 11 4 11 3 7 2 q t q t q t q t

The Euler characteristic of the Khovanov Homology $\operatorname {\it {KH}} (L)$ is (up to normalization) the Jones polynomial $J(L)$ of $L$. Precisely,

$\operatorname {\it {Kh}} (L)(q,-1)={\hat {J}}(L)(q):=(q+q^{-1})J(L)(q^{2})$.

Let us verify this in the case of 5_1:

In[4]:=	{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}
Out[4]=	-15 -7 -5 -3 -15 -7 -5 -3 {-q + q + q + q , -q + q + q + q }

5_1

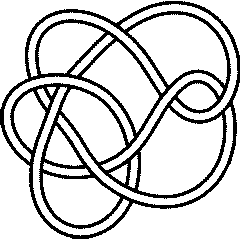10_132

Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, $J(5_{1})=J(10_{132})$ though $\operatorname {\it {Kh}} (5_{1})\neq \operatorname {\it {Kh}} (10_{132})$:

In[5]:=	{ Jones[Knot[5, 1]] === Jones[Knot[10, 132]], Kh[Knot[5, 1]] === Kh[Knot[10, 132]] }
Out[5]=	{True, False}

The algorithm presently used by KnotTheory` is an efficient algorithm modeled on the Kauffman bracket algorithm of The Jones Polynomial, as explained in [Bar-Natan3] (which follows [Bar-Natan2]). Currently, two implementations of this algorithm are available:

• FastKh: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax Kh[L, Program -> "FastKh"][q, t] or by changing the default behaviour of Kh by evaluating SetOptions[Kh, Program -> "FastKh"].
• JavaKh: In the summer of 2005 Jeremy Green re-implemented the algorithm in java (java 1.5 required!) with much further care to the details, leading to an improvemnet factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax Kh[L, Program -> "JavaKh"][q, t].

In[6]:=	Options[Kh]
Out[6]=	{ExpansionOrder -> Automatic, Program -> JavaKh, Modulus -> 0, JavaOptions -> }

JavaKh takes an additional option, Modulus, which sets the characteristic of the ground field for the homology computations to $0$ or to a prime $p$. Thus for example, the following four In lines imply that the Khovanov homology of the torus knot T(6,5) has both 3 torsion and 5 torsion, but no 7 torsion:

In[7]:=

T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];

In[8]:=	Kh[T65, Modulus -> 3][q, t] - kh
Out[8]=	43 13 43 14 q t + q t

In[9]:=	Kh[T65, Modulus -> 5][q, t] - kh
Out[9]=	35 10 35 11 39 11 39 12 q t + q t + q t + q t

In[10]:=	Kh[T65, Modulus -> 7][q, t] - kh
Out[10]=	0

T(6,5)

The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion:

In[11]:= ?JavaOptions JavaOptions is an option to Kh. Kh[L, Program -> "JavaKh", JavaOptions -> jopts] calls java with options jopts. Thus for example, JavaOptions -> "-Xmx256m" sets the maximum java heap size to 256MB - useful for large computations.

In[12]:=

SetOptions[Kh, JavaOptions -> "-Xmx256m"];

In[13]:=

T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];

In[14]:=	Factor[Kh[T87, Modulus -> 3][q, t] - kh]
Out[14]=	79 25 q t (1 + t)

In[15]:=	Factor[Kh[T87, Modulus -> 5][q, t] - kh]
Out[15]=	61 11 12 10 14 12 18 13 q t (1 + t) (1 + q t + q t + q t )

In[16]:=	Factor[Kh[T87, Modulus -> 7][q, t] - kh]
Out[16]=	61 14 8 6 12 7 10 8 14 9 q t (1 + t) (1 + q t + q t + q t + q t )

In[17]:=	Factor[Kh[T87, Modulus -> 11][q, t] - kh]
Out[17]=	0

JavaKh also works over the integers:

In[18]:= ?ZMod ZMod[m] denotes the cyclic group Z/mZ. Thus if m=0 it is the infinite cyclic group Z and if m>0 it is the finite cyclic group with m elements. ZMod[m1, m2, ...] denotes the direct sum of ZMod[m1], ZMod[m2], ... .

For example, the 22nd homology group over ${\mathbb {Z} }$ of the torus knot T(8,7) at degree 73 is the 280 element torsion group ${\mathbb {Z} }_{2}\oplus {\mathbb {Z} }_{4}\oplus {\mathbb {Z} }_{5}\oplus {\mathbb {Z} }_{7}$:

In[19]:=	Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]
Out[19]=	ZMod[2, 4, 5, 7]

T(8,7) is currently not on the Knot Atlas. Let us see what it looks like:

In[20]:=	Show[TubePlot[TorusKnot[8, 7]]]
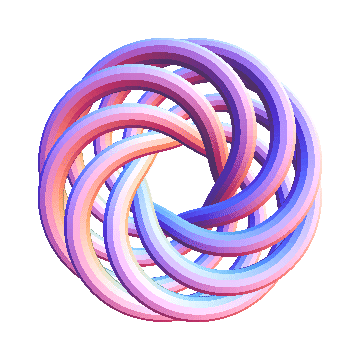
Out[20]=	-Graphics3D-

Finally, JavaKh may also be run outside of Mathematica, as the following example demonstrates:

drorbn@coxeter:.../KnotTheory: cd JavaKh
drorbn@coxeter:.../KnotTheory/JavaKh: java JavaKh
PD[X[3, 1, 4, 6], X[1, 5, 2, 4], X[5, 3, 6, 2]]
"+ q^1t^0 + q^3t^0 + q^5t^2 + q^9t^3 "

(Type java JavaKh -help for some further help).

August 2002, Toronto: Mikhail Khovanov explaining his more recent paper [Khovanov2].

[Bar-Natan1] ^  D. Bar-Natan, On Khovanov's categorification of the Jones polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370, arXiv:math.GT/0201043.

[Bar-Natan2] ^  D. Bar-Natan, Khovanov's Homology for Tangles and Cobordisms, Geometry and Topology 9-33 (2005) 1443-1499, arXiv:math.GT/0410495.

[Bar-Natan3] ^  D. Bar-Natan, I've Computed Kh(T(9,5)) and I'm Happy, talk given at Knots in Washington XX, George Washington University, February 2005.

[Khovanov1] ^  M. Khovanov, A categorification of the Jones polynomial, arXiv:math.QA/9908171.

[Khovanov2] ^  M. Khovanov, An invariant of tangle cobordisms, arXiv:math.QA/0207264.

See also A Khovanov homology bibliography.