Khovanov Homology: Difference between revisions
(Link to java.sun.com added.) |
mNo edit summary |
||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
The Khovanov Homology <math>\operatorname{\it KH}(L)</math> of a knot or a link <math>L</math>, also known as Khovanov's categorification of the Jones polynomial of <math>L</math>, was defined by Khovanov in {{ref|Khovanov1}} (also check {{ref|Bar-Natan1}}), where the notation is closer to the notation used here). It is a graded homology theory; each homology group <math>\operatorname{\it KH}^r(L)</math> is in itself a direct sum <math>\bigoplus_j\operatorname{\it KH}^r_j(L)</math> of homogeneous components. Over a field one can form the two-variable " |
The Khovanov Homology <math>\operatorname{\it KH}(L)</math> of a knot or a link <math>L</math>, also known as Khovanov's categorification of the Jones polynomial of <math>L</math>, was defined by Khovanov in {{ref|Khovanov1}} (also check {{ref|Bar-Natan1}}), where the notation is closer to the notation used here). It is a graded homology theory; each homology group <math>\operatorname{\it KH}^r(L)</math> is in itself a direct sum <math>\bigoplus_j\operatorname{\it KH}^r_j(L)</math> of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" <math>\operatorname{\it Kh}(L)</math> (which deserves the name "the Khovanov polynomial of <math>L</math>"), |
||
<center><math>\operatorname{\it Kh}(L)(q,t) := \sum_{r,j}t^rq^j\dim\operatorname{\it KH}^r_j(L)</math>.</center> |
<center><math>\operatorname{\it Kh}(L)(q,t) := \sum_{r,j}t^rq^j\dim\operatorname{\it KH}^r_j(L)</math>.</center> |
||
Revision as of 10:46, 12 April 2006
The Khovanov Homology of a knot or a link , also known as Khovanov's categorification of the Jones polynomial of , was defined by Khovanov in [Khovanov1] (also check [Bar-Natan1]), where the notation is closer to the notation used here). It is a graded homology theory; each homology group is in itself a direct sum of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" (which deserves the name "the Khovanov polynomial of "),
(For In[1] see Setup)
| ||||
Thus for example, here's the Khovanov polynomial of the knot 5_1:
In[3]:=
|
kh = Kh[Knot[5, 1]][q, t]
|
Out[3]=
|
-5 -3 1 1 1 1
q + q + ------ + ------ + ------ + -----
15 5 11 4 11 3 7 2
q t q t q t q t
|
The Euler characteristic of the Khovanov Homology is (up to normalization) the Jones polynomial of . Precisely,
Let us verify this in the case of 5_1:
In[4]:=
|
{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}
|
Out[4]=
|
-15 -7 -5 -3 -15 -7 -5 -3
{-q + q + q + q , -q + q + q + q }
|
 5_1 |
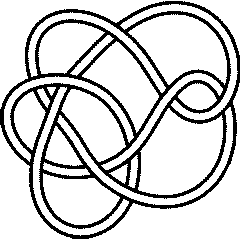 10_132 |
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, though :
In[5]:=
|
{
Jones[Knot[5, 1]] === Jones[Knot[10, 132]],
Kh[Knot[5, 1]] === Kh[Knot[10, 132]]
}
|
Out[5]=
|
{True, False}
|
The algorithm presently used by KnotTheory` is an efficient algorithm modeled on the Kauffman bracket algorithm of The Jones Polynomial, as explained in [Bar-Natan3] (which follows [Bar-Natan2]). Currently, two implementations of this algorithm are available:
- FastKh: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax
Kh[L, Program -> "FastKh"][q, t]or by changing the default behaviour ofKhby evaluatingSetOptions[Kh, Program -> "FastKh"]. - JavaKh: In the summer of 2005 Jeremy Green re-implemented the algorithm in java (java 1.5 required, can be had from http://java.sun.com/) with much further care to the details, leading to an improvement factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax
Kh[L, Program -> "JavaKh"][q, t].
In[6]:=
|
Options[Kh]
|
Out[6]=
|
{ExpansionOrder -> Automatic, Program -> JavaKh, Modulus -> 0,
JavaOptions -> }
|
JavaKh takes an additional option, Modulus, which sets the characteristic of the ground field for the homology computations to or to a prime . Thus for example, the following four In lines imply that the Khovanov homology of the torus knot T(6,5) has both 3 torsion and 5 torsion, but no 7 torsion:
In[7]:=
|
T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];
|
In[8]:=
|
Kh[T65, Modulus -> 3][q, t] - kh
|
Out[8]=
|
43 13 43 14
q t + q t
|
In[9]:=
|
Kh[T65, Modulus -> 5][q, t] - kh
|
Out[9]=
|
35 10 35 11 39 11 39 12
q t + q t + q t + q t
|
In[10]:=
|
Kh[T65, Modulus -> 7][q, t] - kh
|
Out[10]=
|
0
|
 T(6,5) |
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion:
| ||||
In[12]:=
|
SetOptions[Kh, JavaOptions -> "-Xmx256m"];
|
In[13]:=
|
T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];
|
In[14]:=
|
Factor[Kh[T87, Modulus -> 3][q, t] - kh]
|
Out[14]=
|
79 25
q t (1 + t)
|
In[15]:=
|
Factor[Kh[T87, Modulus -> 5][q, t] - kh]
|
Out[15]=
|
61 11 12 10 14 12 18 13
q t (1 + t) (1 + q t + q t + q t )
|
In[16]:=
|
Factor[Kh[T87, Modulus -> 7][q, t] - kh]
|
Out[16]=
|
61 14 8 6 12 7 10 8 14 9
q t (1 + t) (1 + q t + q t + q t + q t )
|
In[17]:=
|
Factor[Kh[T87, Modulus -> 11][q, t] - kh]
|
Out[17]=
|
0
|
JavaKh also works over the integers:
| ||||
For example, the 22nd homology group over of the torus knot T(8,7) at degree 73 is the 280 element torsion group :
In[19]:=
|
Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]
|
Out[19]=
|
ZMod[2, 4, 5, 7]
|
T(8,7) is currently not on the Knot Atlas. Let us see what it looks like:
In[20]:=
|
Show[TubePlot[TorusKnot[8, 7]]]
|
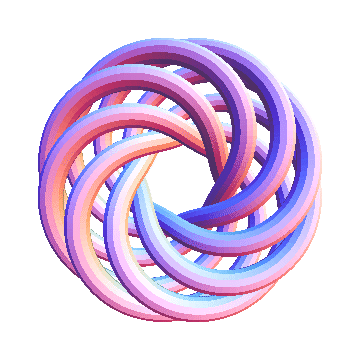
| |
Out[20]=
|
-Graphics3D-
|
Finally, JavaKh may also be run outside of Mathematica, as the following example demonstrates:
drorbn@coxeter:.../KnotTheory: cd JavaKh drorbn@coxeter:.../KnotTheory/JavaKh: java JavaKh PD[X[3, 1, 4, 6], X[1, 5, 2, 4], X[5, 3, 6, 2]] "+ q^1t^0 + q^3t^0 + q^5t^2 + q^9t^3 "
(Type java JavaKh -help for some further help).
[Bar-Natan1] ^ D. Bar-Natan, On Khovanov's categorification of the Jones polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370, arXiv:math.GT/0201043.
[Bar-Natan2] ^ D. Bar-Natan, Khovanov's Homology for Tangles and Cobordisms, Geometry and Topology 9-33 (2005) 1443-1499, arXiv:math.GT/0410495.
[Bar-Natan3] ^ D. Bar-Natan, I've Computed Kh(T(9,5)) and I'm Happy, talk given at Knots in Washington XX, George Washington University, February 2005.
[Khovanov1] ^ M. Khovanov, A categorification of the Jones polynomial, arXiv:math.QA/9908171.
[Khovanov2] ^ M. Khovanov, An invariant of tangle cobordisms, arXiv:math.QA/0207264.
See also A Khovanov homology bibliography.













