Structure and Operations

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

In[1]:= ?Crossings Crossings[L] returns the number of crossings of a knot/link L (in its given presentation).

In[2]:= ?PositiveCrossings PositiveCrossings[L] returns the number of positive (right handed) crossings in a knot/link L (in its given presentation).

In[3]:= ?NegativeCrossings NegativeCrossings[L] returns the number of negaitve (left handed) crossings in a knot/link L (in its given presentation).

Thus here's one tautology and one easy example:

In[4]:=	Crossings /@ {Knot[0, 1], TorusKnot[11,10]}
Out[4]=	{0, 99}

And another easy example:

In[5]:=	K=Knot[6, 2]; {PositiveCrossings[K], NegativeCrossings[K]}
Out[5]=	{2, 4}

In[6]:= ?PositiveQ PositiveQ[xing] returns True if xing is a positive (right handed) crossing and False if it is negative (left handed).

In[7]:= ?NegativeQ NegativeQ[xing] returns True if xing is a negative (left handed) crossing and False if it is positive (right handed).

For example,

In[8]:=	PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}
Out[8]=	{False, True, True, True}

In[9]:= ?ConnectedSum ConnectedSum[K1, K2] represents the connected sum of the knots K1 and K2 (ConnectedSum may not work with links).

The connected sum $K=4_{1}\#4_{1}$ of the knot 4_1 with itself has 8 crossings (unsurprisingly):

In[10]:=	K = ConnectedSum[Knot[4,1], Knot[4,1]]
Out[10]=	ConnectedSum[Knot[4, 1], Knot[4, 1]]

In[11]:=	Crossings[K]
Out[11]=	8

It is also nice to know that, as expected, the Jones polynomial of $K$ is the square of the Jones polynomial of 4_1:

In[12]:=	Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]
Out[12]=	True

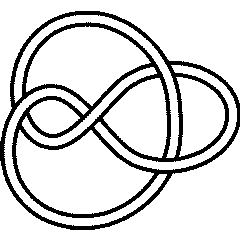4_1

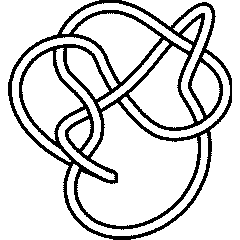8_9

It is less nice to know that the Jones polynomial cannot tell $K$ apart from the knot 8_9:

In[13]:=	Jones[K][q] == Jones[Knot[8,9]][q]
Out[13]=	True

But $K=4_{1}\#4_{1}$ isn't equivalent to 8_9; indeed, their Alexander polynomials are different:

In[14]:=	{Alexander[K][t], Alexander[Knot[8,9]][t]}
Out[14]=	-2 6 2 -3 3 5 2 3 {11 + t - - - 6 t + t , 7 - t + -- - - - 5 t + 3 t - t } t 2 t t