10 141: Difference between revisions
(Resetting knot page to basic template.) |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<!-- WARNING! WARNING! WARNING! |
|||
{{Template:Basic Knot Invariants|name=10_141}} |
|||
<!-- This page was generated from the splice base [[Rolfsen_Splice_Base]]. Please do not edit! |
|||
<!-- You probably want to edit the template referred to immediately below. (See [[Category:Knot Page Template]].) |
|||
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Rolfsen_Splice_Base]]. --> |
|||
<!-- --> |
|||
<!-- --> |
|||
{{Rolfsen Knot Page| |
|||
n = 10 | |
|||
k = 141 | |
|||
KnotilusURL = http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/-1,10,-2,1,3,-5,4,-9,-10,2,-7,8,9,-3,5,-4,-6,7,-8,6/goTop.html | |
|||
braid_table = <table cellspacing=0 cellpadding=0 border=0> |
|||
<tr><td>[[Image:BraidPart1.gif]][[Image:BraidPart1.gif]][[Image:BraidPart1.gif]][[Image:BraidPart1.gif]][[Image:BraidPart0.gif]][[Image:BraidPart3.gif]][[Image:BraidPart3.gif]][[Image:BraidPart3.gif]][[Image:BraidPart0.gif]][[Image:BraidPart0.gif]]</td></tr> |
|||
<tr><td>[[Image:BraidPart2.gif]][[Image:BraidPart2.gif]][[Image:BraidPart2.gif]][[Image:BraidPart2.gif]][[Image:BraidPart3.gif]][[Image:BraidPart4.gif]][[Image:BraidPart4.gif]][[Image:BraidPart4.gif]][[Image:BraidPart3.gif]][[Image:BraidPart3.gif]]</td></tr> |
|||
<tr><td>[[Image:BraidPart0.gif]][[Image:BraidPart0.gif]][[Image:BraidPart0.gif]][[Image:BraidPart0.gif]][[Image:BraidPart4.gif]][[Image:BraidPart0.gif]][[Image:BraidPart0.gif]][[Image:BraidPart0.gif]][[Image:BraidPart4.gif]][[Image:BraidPart4.gif]]</td></tr> |
|||
</table> | |
|||
braid_crossings = 10 | |
|||
braid_width = 3 | |
|||
braid_index = 3 | |
|||
same_alexander = [[8_5]], | |
|||
same_jones = | |
|||
khovanov_table = <table border=1> |
|||
<tr align=center> |
|||
<td width=15.3846%><table cellpadding=0 cellspacing=0> |
|||
<tr><td>\</td><td> </td><td>r</td></tr> |
|||
<tr><td> </td><td> \ </td><td> </td></tr> |
|||
<tr><td>j</td><td> </td><td>\</td></tr> |
|||
</table></td> |
|||
<td width=7.69231%>-6</td ><td width=7.69231%>-5</td ><td width=7.69231%>-4</td ><td width=7.69231%>-3</td ><td width=7.69231%>-2</td ><td width=7.69231%>-1</td ><td width=7.69231%>0</td ><td width=7.69231%>1</td ><td width=7.69231%>2</td ><td width=15.3846%>χ</td></tr> |
|||
<tr align=center><td>5</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td bgcolor=yellow>1</td><td>1</td></tr> |
|||
<tr align=center><td>3</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td bgcolor=yellow>1</td><td bgcolor=yellow> </td><td>-1</td></tr> |
|||
<tr align=center><td>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td bgcolor=yellow>2</td><td bgcolor=yellow>1</td><td> </td><td>1</td></tr> |
|||
<tr align=center><td>-1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td bgcolor=yellow>2</td><td bgcolor=yellow>2</td><td> </td><td> </td><td>0</td></tr> |
|||
<tr align=center><td>-3</td><td> </td><td> </td><td> </td><td> </td><td bgcolor=yellow>2</td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td>1</td></tr> |
|||
<tr align=center><td>-5</td><td> </td><td> </td><td> </td><td bgcolor=yellow>1</td><td bgcolor=yellow>2</td><td> </td><td> </td><td> </td><td> </td><td>1</td></tr> |
|||
<tr align=center><td>-7</td><td> </td><td> </td><td bgcolor=yellow>1</td><td bgcolor=yellow>2</td><td> </td><td> </td><td> </td><td> </td><td> </td><td>-1</td></tr> |
|||
<tr align=center><td>-9</td><td> </td><td bgcolor=yellow>1</td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>0</td></tr> |
|||
<tr align=center><td>-11</td><td bgcolor=yellow> </td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>-1</td></tr> |
|||
<tr align=center><td>-13</td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>1</td></tr> |
|||
</table> | |
|||
coloured_jones_2 = <math>q^6-q^5+q^3-3 q^2+3 q+1-6 q^{-1} +6 q^{-2} +3 q^{-3} -8 q^{-4} +4 q^{-5} +6 q^{-6} -9 q^{-7} + q^{-8} +7 q^{-9} -8 q^{-10} - q^{-11} +8 q^{-12} -4 q^{-13} -3 q^{-14} +5 q^{-15} - q^{-16} -2 q^{-17} + q^{-18} </math> | |
|||
coloured_jones_3 = <math>2 q^{12}-2 q^{11}-2 q^{10}-q^9+6 q^8+2 q^7-6 q^6-7 q^5+6 q^4+12 q^3-3 q^2-17 q+18 q^{-1} +6 q^{-2} -20 q^{-3} -6 q^{-4} +17 q^{-5} +9 q^{-6} -16 q^{-7} -6 q^{-8} +11 q^{-9} +7 q^{-10} -10 q^{-11} -4 q^{-12} +4 q^{-13} +4 q^{-14} - q^{-15} -3 q^{-16} -4 q^{-17} + q^{-18} +8 q^{-19} +2 q^{-20} -8 q^{-21} -6 q^{-22} +9 q^{-23} +8 q^{-24} -6 q^{-25} -10 q^{-26} +2 q^{-27} +9 q^{-28} + q^{-29} -7 q^{-30} -2 q^{-31} +4 q^{-32} +2 q^{-33} - q^{-34} -2 q^{-35} + q^{-36} </math> | |
|||
coloured_jones_4 = <math>q^{21}+q^{20}-4 q^{19}-q^{18}+q^{17}+6 q^{16}+5 q^{15}-13 q^{14}-7 q^{13}-q^{12}+21 q^{11}+21 q^{10}-23 q^9-29 q^8-20 q^7+40 q^6+57 q^5-16 q^4-56 q^3-57 q^2+43 q+91+7 q^{-1} -63 q^{-2} -87 q^{-3} +28 q^{-4} +104 q^{-5} +26 q^{-6} -54 q^{-7} -95 q^{-8} +16 q^{-9} +100 q^{-10} +25 q^{-11} -42 q^{-12} -87 q^{-13} +8 q^{-14} +89 q^{-15} +21 q^{-16} -30 q^{-17} -75 q^{-18} -4 q^{-19} +75 q^{-20} +20 q^{-21} -12 q^{-22} -57 q^{-23} -19 q^{-24} +51 q^{-25} +15 q^{-26} +9 q^{-27} -30 q^{-28} -24 q^{-29} +23 q^{-30} - q^{-31} +18 q^{-32} -3 q^{-33} -14 q^{-34} +9 q^{-35} -21 q^{-36} +8 q^{-37} +8 q^{-38} +3 q^{-39} +16 q^{-40} -25 q^{-41} -6 q^{-42} +5 q^{-44} +24 q^{-45} -10 q^{-46} -7 q^{-47} -9 q^{-48} -4 q^{-49} +17 q^{-50} -5 q^{-53} -6 q^{-54} +5 q^{-55} + q^{-56} +2 q^{-57} - q^{-58} -2 q^{-59} + q^{-60} </math> | |
|||
coloured_jones_5 = <math>q^{32}-4 q^{29}+2 q^{27}+3 q^{26}+2 q^{25}-2 q^{24}-8 q^{23}+q^{22}+11 q^{21}+5 q^{20}-3 q^{19}-17 q^{18}-22 q^{17}+7 q^{16}+43 q^{15}+40 q^{14}-6 q^{13}-64 q^{12}-81 q^{11}-14 q^{10}+97 q^9+131 q^8+42 q^7-113 q^6-186 q^5-86 q^4+115 q^3+234 q^2+137 q-104-267 q^{-1} -178 q^{-2} +82 q^{-3} +275 q^{-4} +214 q^{-5} -55 q^{-6} -279 q^{-7} -228 q^{-8} +37 q^{-9} +266 q^{-10} +234 q^{-11} -21 q^{-12} -258 q^{-13} -227 q^{-14} +15 q^{-15} +241 q^{-16} +226 q^{-17} -12 q^{-18} -232 q^{-19} -214 q^{-20} +2 q^{-21} +212 q^{-22} +214 q^{-23} +11 q^{-24} -196 q^{-25} -208 q^{-26} -29 q^{-27} +165 q^{-28} +205 q^{-29} +56 q^{-30} -138 q^{-31} -195 q^{-32} -74 q^{-33} +96 q^{-34} +176 q^{-35} +101 q^{-36} -58 q^{-37} -154 q^{-38} -104 q^{-39} +16 q^{-40} +112 q^{-41} +111 q^{-42} +19 q^{-43} -78 q^{-44} -92 q^{-45} -39 q^{-46} +31 q^{-47} +68 q^{-48} +46 q^{-49} -2 q^{-50} -36 q^{-51} -36 q^{-52} -14 q^{-53} +6 q^{-54} +17 q^{-55} +16 q^{-56} +9 q^{-57} +6 q^{-58} -4 q^{-59} -13 q^{-60} -17 q^{-61} -11 q^{-62} +2 q^{-63} +21 q^{-64} +21 q^{-65} +6 q^{-66} -9 q^{-67} -21 q^{-68} -19 q^{-69} - q^{-70} +17 q^{-71} +17 q^{-72} +8 q^{-73} -3 q^{-74} -15 q^{-75} -12 q^{-76} +8 q^{-78} +7 q^{-79} +4 q^{-80} -7 q^{-82} -4 q^{-83} + q^{-84} +2 q^{-85} + q^{-86} +2 q^{-87} - q^{-88} -2 q^{-89} + q^{-90} </math> | |
|||
coloured_jones_6 = <math>q^{45}+q^{44}-2 q^{43}-q^{42}-4 q^{41}+q^{40}+2 q^{39}+4 q^{38}+9 q^{37}-3 q^{36}-2 q^{35}-14 q^{34}-3 q^{33}-6 q^{32}+q^{31}+23 q^{30}+10 q^{29}+17 q^{28}-9 q^{27}-q^{26}-41 q^{25}-49 q^{24}-5 q^{23}+11 q^{22}+71 q^{21}+77 q^{20}+92 q^{19}-45 q^{18}-151 q^{17}-159 q^{16}-122 q^{15}+67 q^{14}+228 q^{13}+352 q^{12}+120 q^{11}-177 q^{10}-377 q^9-426 q^8-127 q^7+281 q^6+646 q^5+435 q^4-13 q^3-467 q^2-711 q-430+151 q^{-1} +768 q^{-2} +683 q^{-3} +224 q^{-4} -379 q^{-5} -805 q^{-6} -632 q^{-7} -25 q^{-8} +719 q^{-9} +748 q^{-10} +357 q^{-11} -260 q^{-12} -760 q^{-13} -673 q^{-14} -109 q^{-15} +645 q^{-16} +709 q^{-17} +372 q^{-18} -207 q^{-19} -700 q^{-20} -643 q^{-21} -123 q^{-22} +598 q^{-23} +662 q^{-24} +360 q^{-25} -173 q^{-26} -648 q^{-27} -617 q^{-28} -154 q^{-29} +528 q^{-30} +617 q^{-31} +383 q^{-32} -90 q^{-33} -561 q^{-34} -597 q^{-35} -243 q^{-36} +387 q^{-37} +547 q^{-38} +435 q^{-39} +60 q^{-40} -410 q^{-41} -556 q^{-42} -366 q^{-43} +171 q^{-44} +417 q^{-45} +467 q^{-46} +242 q^{-47} -186 q^{-48} -444 q^{-49} -456 q^{-50} -74 q^{-51} +202 q^{-52} +404 q^{-53} +371 q^{-54} +65 q^{-55} -226 q^{-56} -415 q^{-57} -247 q^{-58} -49 q^{-59} +208 q^{-60} +345 q^{-61} +226 q^{-62} +27 q^{-63} -221 q^{-64} -236 q^{-65} -195 q^{-66} -20 q^{-67} +162 q^{-68} +194 q^{-69} +159 q^{-70} -15 q^{-71} -76 q^{-72} -145 q^{-73} -110 q^{-74} -13 q^{-75} +42 q^{-76} +106 q^{-77} +38 q^{-78} +43 q^{-79} -12 q^{-80} -39 q^{-81} -36 q^{-82} -38 q^{-83} +12 q^{-84} -32 q^{-85} +24 q^{-86} +27 q^{-87} +29 q^{-88} +21 q^{-89} -2 q^{-90} +13 q^{-91} -61 q^{-92} -26 q^{-93} -15 q^{-94} +9 q^{-95} +21 q^{-96} +27 q^{-97} +49 q^{-98} -20 q^{-99} -15 q^{-100} -28 q^{-101} -17 q^{-102} -13 q^{-103} +5 q^{-104} +40 q^{-105} +4 q^{-106} +9 q^{-107} -6 q^{-108} -8 q^{-109} -17 q^{-110} -10 q^{-111} +13 q^{-112} + q^{-113} +8 q^{-114} +3 q^{-115} +3 q^{-116} -7 q^{-117} -6 q^{-118} +3 q^{-119} -2 q^{-120} +2 q^{-121} + q^{-122} +2 q^{-123} - q^{-124} -2 q^{-125} + q^{-126} </math> | |
|||
coloured_jones_7 = | |
|||
computer_talk = |
|||
<table> |
|||
<tr valign=top> |
|||
<td><pre style="color: blue; border: 0px; padding: 0em">In[1]:= </pre></td> |
|||
<td align=left><pre style="color: red; border: 0px; padding: 0em"><< KnotTheory`</pre></td> |
|||
</tr> |
|||
<tr valign=top><td colspan=2><nowiki>Loading KnotTheory` (version of August 29, 2005, 15:33:11)...</nowiki></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[2]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>PD[Knot[10, 141]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[2]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>PD[X[1, 4, 2, 5], X[3, 10, 4, 11], X[14, 6, 15, 5], X[16, 8, 17, 7], |
|||
X[6, 16, 7, 15], X[17, 20, 18, 1], X[11, 18, 12, 19], |
|||
X[19, 12, 20, 13], X[8, 14, 9, 13], X[9, 2, 10, 3]]</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[3]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>GaussCode[Knot[10, 141]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[3]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>GaussCode[-1, 10, -2, 1, 3, -5, 4, -9, -10, 2, -7, 8, 9, -3, 5, -4, -6, |
|||
7, -8, 6]</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[4]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>DTCode[Knot[10, 141]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[4]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>DTCode[4, 10, -14, -16, 2, 18, -8, -6, 20, 12]</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[5]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>br = BR[Knot[10, 141]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[5]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>BR[3, {1, 1, 1, 1, -2, -1, -1, -1, -2, -2}]</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[6]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{First[br], Crossings[br]}</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[6]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{3, 10}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[7]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>BraidIndex[Knot[10, 141]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[7]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>3</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[8]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Show[DrawMorseLink[Knot[10, 141]]]</nowiki></code></td></tr> |
|||
<tr align=left><td></td><td>[[Image:10_141_ML.gif]]</td></tr><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[8]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>-Graphics-</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[9]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> (#[Knot[10, 141]]&) /@ { |
|||
SymmetryType, UnknottingNumber, ThreeGenus, |
|||
BridgeIndex, SuperBridgeIndex, NakanishiIndex |
|||
}</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[9]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{Reversible, 1, 3, 3, NotAvailable, 1}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[10]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>alex = Alexander[Knot[10, 141]][t]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[10]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> -3 3 4 2 3 |
|||
5 - t + -- - - - 4 t + 3 t - t |
|||
2 t |
|||
t</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[11]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Conway[Knot[10, 141]][z]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[11]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> 2 4 6 |
|||
1 - z - 3 z - z</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[12]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Select[AllKnots[], (alex === Alexander[#][t])&]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[12]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{Knot[8, 5], Knot[10, 141]}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[13]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{KnotDet[Knot[10, 141]], KnotSignature[Knot[10, 141]]}</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[13]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{21, 0}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[14]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Jones[Knot[10, 141]][q]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[14]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> -6 2 2 3 4 3 2 |
|||
3 + q - -- + -- - -- + -- - - - 2 q + q |
|||
5 4 3 2 q |
|||
q q q q</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[15]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[15]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{Knot[10, 141]}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[16]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>A2Invariant[Knot[10, 141]][q]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[16]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> -18 -12 -10 -8 -4 2 6 |
|||
q - q - q + q + q + q + q</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[17]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>HOMFLYPT[Knot[10, 141]][a, z]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[17]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> 2 4 2 2 2 4 2 4 2 4 4 4 2 6 |
|||
2 - 2 a + a + 3 z - 7 a z + 3 a z + z - 5 a z + a z - a z</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[18]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Kauffman[Knot[10, 141]][a, z]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[18]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> 2 |
|||
2 4 z 3 5 2 z 2 2 |
|||
2 + 2 a + a - - - 3 a z - 4 a z - 2 a z - 4 z + -- - 9 a z - |
|||
a 2 |
|||
a |
|||
3 |
|||
4 2 6 2 2 z 3 3 3 5 3 4 |
|||
a z + 3 a z + ---- + 5 a z + 13 a z + 10 a z + 3 z + |
|||
a |
|||
2 4 4 4 6 4 5 3 5 5 5 2 6 |
|||
8 a z + a z - 4 a z - 3 a z - 12 a z - 9 a z - 4 a z - |
|||
4 6 6 6 7 3 7 5 7 2 8 4 8 |
|||
3 a z + a z + a z + 3 a z + 2 a z + a z + a z</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[19]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{Vassiliev[2][Knot[10, 141]], Vassiliev[3][Knot[10, 141]]}</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[19]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>{-1, 1}</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[20]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Kh[Knot[10, 141]][q, t]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[20]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>2 1 1 1 1 1 2 1 |
|||
- + 2 q + ------ + ------ + ----- + ----- + ----- + ----- + ----- + |
|||
q 13 6 11 5 9 5 9 4 7 4 7 3 5 3 |
|||
q t q t q t q t q t q t q t |
|||
2 2 1 2 3 5 2 |
|||
----- + ----- + ---- + --- + q t + q t + q t |
|||
5 2 3 2 3 q t |
|||
q t q t q t</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[21]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>ColouredJones[Knot[10, 141], 2][q]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[21]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> -18 2 -16 5 3 4 8 -11 8 7 -8 |
|||
1 + q - --- - q + --- - --- - --- + --- - q - --- + -- + q - |
|||
17 15 14 13 12 10 9 |
|||
q q q q q q q |
|||
9 6 4 8 3 6 6 2 3 5 6 |
|||
-- + -- + -- - -- + -- + -- - - + 3 q - 3 q + q - q + q |
|||
7 6 5 4 3 2 q |
|||
q q q q q q</nowiki></code></td></tr> |
|||
</table> }} |
|||
Latest revision as of 18:06, 1 September 2005
|
|
|
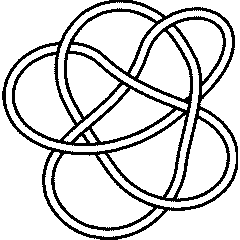 (KnotPlot image) |
See the full Rolfsen Knot Table. Visit 10 141's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) |
Knot presentations
| Planar diagram presentation | X1425 X3,10,4,11 X14,6,15,5 X16,8,17,7 X6,16,7,15 X17,20,18,1 X11,18,12,19 X19,12,20,13 X8,14,9,13 X9,2,10,3 |
| Gauss code | -1, 10, -2, 1, 3, -5, 4, -9, -10, 2, -7, 8, 9, -3, 5, -4, -6, 7, -8, 6 |
| Dowker-Thistlethwaite code | 4 10 -14 -16 2 18 -8 -6 20 12 |
| Conway Notation | [4,21,21-] |
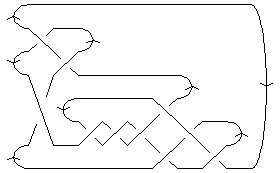
| Minimum Braid Representative | A Morse Link Presentation | An Arc Presentation | |||
Length is 10, width is 3, Braid index is 3 |
|
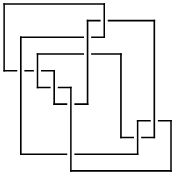 [{11, 5}, {2, 9}, {8, 10}, {9, 11}, {6, 4}, {5, 3}, {4, 1}, {3, 8}, {7, 2}, {10, 6}, {1, 7}] |
[edit Notes on presentations of 10 141]
KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of May 31, 2006, 14:15:20.091.
|
In[3]:=
|
K = Knot["10 141"];
|
In[4]:=
|
PD[K]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
X1425 X3,10,4,11 X14,6,15,5 X16,8,17,7 X6,16,7,15 X17,20,18,1 X11,18,12,19 X19,12,20,13 X8,14,9,13 X9,2,10,3 |
In[5]:=
|
GaussCode[K]
|
Out[5]=
|
-1, 10, -2, 1, 3, -5, 4, -9, -10, 2, -7, 8, 9, -3, 5, -4, -6, 7, -8, 6 |
In[6]:=
|
DTCode[K]
|
Out[6]=
|
4 10 -14 -16 2 18 -8 -6 20 12 |
(The path below may be different on your system)
In[7]:=
|
AppendTo[$Path, "C:/bin/LinKnot/"];
|
In[8]:=
|
ConwayNotation[K]
|
Out[8]=
|
[4,21,21-] |
In[9]:=
|
br = BR[K]
|
KnotTheory::credits: The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See arXiv:math.GT/0401051.
|
Out[9]=
|
In[10]:=
|
{First[br], Crossings[br], BraidIndex[K]}
|
KnotTheory::credits: The braid index data known to KnotTheory` is taken from Charles Livingston's http://www.indiana.edu/~knotinfo/.
|
KnotTheory::loading: Loading precomputed data in IndianaData`.
|
Out[10]=
|
{ 3, 10, 3 } |
In[11]:=
|
Show[BraidPlot[br]]
|
Out[11]=
|
-Graphics- |
In[12]:=
|
Show[DrawMorseLink[K]]
|
KnotTheory::credits: "MorseLink was added to KnotTheory` by Siddarth Sankaran at the University of Toronto in the summer of 2005."
|
KnotTheory::credits: "DrawMorseLink was written by Siddarth Sankaran at the University of Toronto in the summer of 2005."
|

|
Out[12]=
|
-Graphics- |
In[13]:=
|
ap = ArcPresentation[K]
|
Out[13]=
|
ArcPresentation[{11, 5}, {2, 9}, {8, 10}, {9, 11}, {6, 4}, {5, 3}, {4, 1}, {3, 8}, {7, 2}, {10, 6}, {1, 7}] |
In[14]:=
|
Draw[ap]
|

|
Out[14]=
|
-Graphics- |
Three dimensional invariants
|
Four dimensional invariants
|
Polynomial invariants
A1 Invariants.
| Weight | Invariant |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 5 | |
| 6 |
A2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 | |
| 1,1 | |
| 2,0 |
A3 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0 | |
| 1,0,0 | |
| 1,0,1 |
A4 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0,0 | |
| 1,0,0,0 |
B2 Invariants.
| Weight | Invariant |
|---|---|
| 0,1 | |
| 1,0 |
D4 Invariants.
| Weight | Invariant |
|---|---|
| 1,0,0,0 |
G2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 |
.
KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of August 31, 2006, 11:25:27.5625.
|
In[3]:=
|
K = Knot["10 141"];
|
In[4]:=
|
Alexander[K][t]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
In[5]:=
|
Conway[K][z]
|
Out[5]=
|
In[6]:=
|
Alexander[K, 2][t]
|
KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.
|
Out[6]=
|
In[7]:=
|
{KnotDet[K], KnotSignature[K]}
|
Out[7]=
|
{ 21, 0 } |
In[8]:=
|
Jones[K][q]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[8]=
|
In[9]:=
|
HOMFLYPT[K][a, z]
|
KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.
|
Out[9]=
|
In[10]:=
|
Kauffman[K][a, z]
|
KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.
|
Out[10]=
|
"Similar" Knots (within the Atlas)
Same Alexander/Conway Polynomial: {8_5,}
Same Jones Polynomial (up to mirroring, ): {}
KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of May 31, 2006, 14:15:20.091.
|
In[3]:=
|
K = Knot["10 141"];
|
In[4]:=
|
{A = Alexander[K][t], J = Jones[K][q]}
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[4]=
|
{ , } |
In[5]:=
|
DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]
|
KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.
|
KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.
|
Out[5]=
|
{8_5,} |
In[6]:=
|
DeleteCases[
Select[
AllKnots[],
(J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) &
],
K
]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots11`.
|
Out[6]=
|
{} |
Vassiliev invariants
| V2 and V3: | (-1, 1) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). The squares with yellow highlighting are those on the "critical diagonals", where or , where 0 is the signature of 10 141. Nonzero entries off the critical diagonals (if any exist) are highlighted in red. |
|
| Integral Khovanov Homology
(db, data source) |
|
The Coloured Jones Polynomials
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session, or any of the Computer Talk sections above.
Modifying This Page
| Read me first: Modifying Knot Pages
See/edit the Rolfsen Knot Page master template (intermediate). See/edit the Rolfsen_Splice_Base (expert). Back to the top. |
|
















































































