Drawing with TubePlot: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| (13 intermediate revisions by 7 users not shown) | |||
| Line 6: | Line 6: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 2 | |
||
in = <nowiki>TubePlot</nowiki> | |
in = <nowiki>TubePlot</nowiki> | |
||
out= <nowiki>TubePlot[gamma, {t, t0, t1}, r, opts] plots the space curve gamma with the variable t running from t0 to t1, as a tube of radius r. The available options are TubeSubdivision, TubeFraming and TubePlotPrelude. All other options are passed on to Graphics3D. TubePlot[TorusKnot[m, n], opts] produces a tube plot of the (m,n) torus knot.</nowiki>}} |
out= <nowiki>TubePlot[gamma, {t, t0, t1}, r, opts] plots the space curve gamma with the variable t running from t0 to t1, as a tube of radius r. The available options are TubeSubdivision, TubeFraming and TubePlotPrelude. All other options are passed on to Graphics3D. TubePlot[TorusKnot[m, n], opts] produces a tube plot of the (m,n) torus knot.</nowiki>}} |
||
| Line 18: | Line 18: | ||
n = 3 | |
n = 3 | |
||
in = <nowiki>Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]</nowiki> | |
in = <nowiki>Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]</nowiki> | |
||
img= |
img= Drawing_with_TubePlot_Out_3.gif | |
||
out= <nowiki>-Graphics3D-</nowiki>}} |
out= <nowiki>-Graphics3D-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 53: | Line 53: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 7 | |
||
in = <nowiki>Show[TubePlot[ |
in = <nowiki>Show[TubePlot[ |
||
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3} |
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3} |
||
| Line 70: | Line 70: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 8 | |
||
in = <nowiki>Show[TubePlot[ |
in = <nowiki>Show[TubePlot[ |
||
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2, |
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2, |
||
| Line 76: | Line 76: | ||
TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]} |
TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]} |
||
]]</nowiki> | |
]]</nowiki> | |
||
img= |
img= Drawing_with_TubePlot_Out_8.gif | |
||
out= <nowiki>-Graphics3D-</nowiki>}} |
out= <nowiki>-Graphics3D-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 92: | Line 92: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 9 | |
||
in = <nowiki>Show[TubePlot[ |
in = <nowiki>Show[TubePlot[ |
||
{Cos[2t], Sin[2t], 0} + |
{Cos[2t], Sin[2t], 0} + |
||
| Line 101: | Line 101: | ||
Boxed -> False, ViewPoint -> {0,0,1} |
Boxed -> False, ViewPoint -> {0,0,1} |
||
]]</nowiki> | |
]]</nowiki> | |
||
img= |
img= Drawing_with_TubePlot_Out_9.gif | |
||
out= <nowiki>-Graphics3D-</nowiki>}} |
out= <nowiki>-Graphics3D-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 110: | Line 110: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 10 | |
||
in = <nowiki>Show[TubePlot[TorusKnot[3, 5]]]</nowiki> | |
in = <nowiki>Show[TubePlot[TorusKnot[3, 5]]]</nowiki> | |
||
img= |
img= Drawing_with_TubePlot_Out_10.gif | |
||
out= <nowiki>-Graphics3D-</nowiki>}} |
out= <nowiki>-Graphics3D-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 120: | Line 120: | ||
</span> |
</span> |
||
There may be some independent interest in the routine <code>TubePlot</code>, and hence it is available also as an independent package. Here it is: [[Media:TubePlot.m|TubePlot.m]]. |
There may be some independent interest in the routine <code>TubePlot</code>, and hence it is available also as an independent package. Here it is: [[Media:TubePlot.m|TubePlot.m]] ([[Image:TubePlot.m|file description]]). |
||
Latest revision as of 17:24, 21 February 2013
(For In[1] see Setup)
| ||||
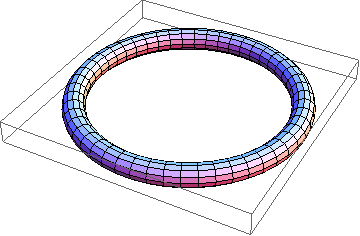
Thus here's a thin unknot:
In[3]:=
|
Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]
|
| |
Out[3]=
|
-Graphics3D-
|
| ||||
| ||||
| ||||
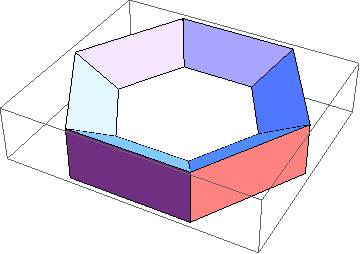
Here's the same unknot, made thicker and not as smooth:
In[7]:=
|
Show[TubePlot[
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3}
]]
|
| |
Out[7]=
|
-Graphics3D-
|
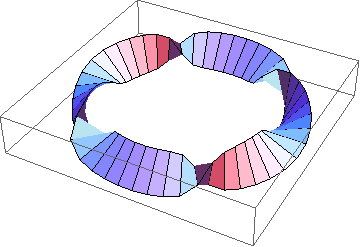
Let's play with the framing now:
In[8]:=
|
Show[TubePlot[
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2,
TubeSubdivision -> {50, 2},
TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]}
]]
|
| |
Out[8]=
|
-Graphics3D-
|
Here's an example that uses a prelude and passes options on to Graphics3D:
The last example serves as the basis for the definition of TubePlot[TorusKnot[m, n]]. Here's a final example:
In[10]:=
|
Show[TubePlot[TorusKnot[3, 5]]]
|
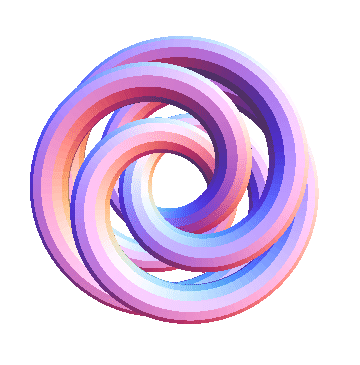
| |
Out[10]=
|
-Graphics3D-
|
Standalone TubePlot
There may be some independent interest in the routine TubePlot, and hence it is available also as an independent package. Here it is: TubePlot.m (File:TubePlot.m).
