Braid Representatives: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
<!--$$?BR$$--> |
<!--$$?BR$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{HelpAndAbout1|n= |
{{HelpAndAbout1|n=1|s=BR}} |
||
BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot. |
BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot. |
||
{{HelpAndAbout2|n= |
{{HelpAndAbout2|n=2|s=BR}} |
||
The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. Vogel's algorithm was implemented by Dan Carney in the summer of 2005 at the University of Toronto. |
The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. Vogel's algorithm was implemented by Dan Carney in the summer of 2005 at the University of Toronto. |
||
{{HelpAndAbout3}} |
{{HelpAndAbout3}} |
||
| Line 15: | Line 15: | ||
<!--$$?Mirror$$--> |
<!--$$?Mirror$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{Help1|n= |
{{Help1|n=3|s=Mirror}} |
||
Mirror[br] return the mirror braid of br. |
Mirror[br] return the mirror braid of br. |
||
{{Help2}} |
{{Help2}} |
||
| Line 24: | Line 24: | ||
<!--$$br1 = BR[2, {-1, -1, -1}];$$--> |
<!--$$br1 = BR[2, {-1, -1, -1}];$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{In1|n= |
{{In1|n=4}} |
||
br1 = BR[2, {-1, -1, -1}]; |
<pre style="color: red; border: 0px; padding: 0em"><nowiki>br1 = BR[2, {-1, -1, -1}];</nowiki></pre> |
||
{{In2}} |
{{In2}} |
||
<!--END--> |
<!--END--> |
||
| Line 32: | Line 32: | ||
<!--$$PD[br1]$$--> |
<!--$$PD[br1]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n= |
{{InOut1|n=5}} |
||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>PD[br1]</nowiki></pre> |
|||
PD[br1] |
|||
{{InOut2|n= |
{{InOut2|n=5}}<pre style="border: 0px; padding: 0em"><nowiki>PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]</nowiki></pre> |
||
{{InOut3}} |
{{InOut3}} |
||
<!--END--> |
<!--END--> |
||
<!--$$Jones[br1][q]$$--> |
<!--$$Jones[br1][q]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n= |
{{InOut1|n=6}} |
||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>Jones[br1][q]</nowiki></pre> |
|||
Jones[br1][q] |
|||
{{InOut2|n= |
{{InOut2|n=6}}<pre style="border: 0px; padding: 0em"><nowiki> -4 -3 1 |
||
-q + q + - |
-q + q + - |
||
q</pre> |
q</nowiki></pre> |
||
{{InOut3}} |
{{InOut3}} |
||
<!--END--> |
<!--END--> |
||
<!--$$Mirror[br1]$$--> |
<!--$$Mirror[br1]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n= |
{{InOut1|n=7}} |
||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>Mirror[br1]</nowiki></pre> |
|||
Mirror[br1] |
|||
{{InOut2|n= |
{{InOut2|n=7}}<pre style="border: 0px; padding: 0em"><nowiki>BR[2, {1, 1, 1}]</nowiki></pre> |
||
{{InOut3}} |
{{InOut3}} |
||
<!--END--> |
<!--END--> |
||
| Line 60: | Line 60: | ||
<!--$$BR[TorusKnot[5, 4]]$$--> |
<!--$$BR[TorusKnot[5, 4]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n= |
{{InOut1|n=8}} |
||
BR[TorusKnot[5, 4]] |
<pre style="color: red; border: 0px; padding: 0em"><nowiki>BR[TorusKnot[5, 4]]</nowiki></pre> |
||
{{InOut2|n= |
{{InOut2|n=8}}<pre style="border: 0px; padding: 0em"><nowiki>BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]</nowiki></pre> |
||
{{InOut3}} |
{{InOut3}} |
||
<!--END--> |
<!--END--> |
||
| Line 70: | Line 70: | ||
<!--$$br2 = BR[Knot[10, 1]]$$--> |
<!--$$br2 = BR[Knot[10, 1]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut1|n= |
{{InOut1|n=9}} |
||
br2 = BR[Knot[10, 1]] |
<pre style="color: red; border: 0px; padding: 0em"><nowiki>br2 = BR[Knot[10, 1]]</nowiki></pre> |
||
{{InOut2|n= |
{{InOut2|n=9}}<pre style="border: 0px; padding: 0em"><nowiki>BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]</nowiki></pre> |
||
{{InOut3}} |
{{InOut3}} |
||
<!--END--> |
<!--END--> |
||
<!--$$Show[BraidPlot[CollapseBraid[br2]]]$$--> |
<!--$$Show[BraidPlot[CollapseBraid[br2]]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{Graphics1|n= |
{{Graphics1|n=10}} |
||
Show[BraidPlot[CollapseBraid[br2]]] |
Show[BraidPlot[CollapseBraid[br2]]] |
||
{{Graphics2|n= |
{{Graphics2|n=10|imagename=Braid_Representatives_Out_10.gif}} |
||
<!--END--> |
<!--END--> |
||
Revision as of 20:41, 27 August 2005
Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:
(For In[1] see Setup)
In[1]:= ?BR
BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot. |
In[2]:= BR::about
The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. Vogel's algorithm was implemented by Dan Carney in the summer of 2005 at the University of Toronto. |
In[3]:= ?Mirror
Mirror[br] return the mirror braid of br. |
Thus for example,
| In[4]:= |
br1 = BR[2, {-1, -1, -1}];
|
| In[5]:= |
PD[br1] |
| Out[5]= | PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]] |
| In[6]:= |
Jones[br1][q] |
| Out[6]= | -4 -3 1
-q + q + -
q
|
| In[7]:= |
Mirror[br1] |
| Out[7]= | BR[2, {1, 1, 1}]
|
KnotTheory` has the braid representatives of some knots and links pre-loaded. Thus for example,
| In[8]:= |
BR[TorusKnot[5, 4]] |
| Out[8]= | BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot Template:10 1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):
| In[9]:= |
br2 = BR[Knot[10, 1]] |
| Out[9]= | BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]
|
| In[10]:= |
Show[BraidPlot[CollapseBraid[br2]]] |
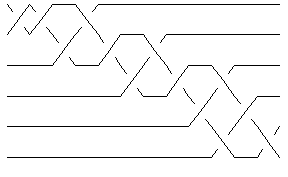
| |
| Out[10]= | -Graphics- |
(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)
[Gittings] ^ T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.