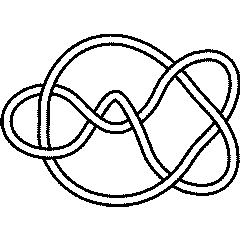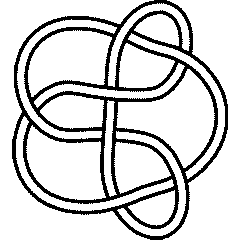7 6: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<!-- --> |
<!-- --> |
||
<!-- --> |
|||
<!-- --> |
|||
<!-- --> |
|||
<!-- provide an anchor so we can return to the top of the page --> |
<!-- provide an anchor so we can return to the top of the page --> |
||
<span id="top"></span> |
<span id="top"></span> |
||
<!-- --> |
|||
<!-- this relies on transclusion for next and previous links --> |
<!-- this relies on transclusion for next and previous links --> |
||
{{Knot Navigation Links|ext=gif}} |
{{Knot Navigation Links|ext=gif}} |
||
| ⚫ | |||
{| align=left |
|||
|- valign=top |
|||
|[[Image:{{PAGENAME}}.gif]] |
|||
| ⚫ | |||
|{{:{{PAGENAME}} Quick Notes}} |
|||
|} |
|||
<br style="clear:both" /> |
<br style="clear:both" /> |
||
| Line 24: | Line 21: | ||
{{Vassiliev Invariants}} |
{{Vassiliev Invariants}} |
||
{{Khovanov Homology|table=<table border=1> |
|||
The coefficients of the monomials <math>t^rq^j</math> are shown, along with their alternating sums <math>\chi</math> (fixed <math>j</math>, alternation over <math>r</math>). The squares with <font class=HLYellow>yellow</font> highlighting are those on the "critical diagonals", where <math>j-2r=s+1</math> or <math>j-2r=s+1</math>, where <math>s=</math>{{Data:{{PAGENAME}}/Signature}} is the signature of {{PAGENAME}}. Nonzero entries off the critical diagonals (if any exist) are highlighted in <font class=HLRed>red</font>. |
|||
<center><table border=1> |
|||
<tr align=center> |
<tr align=center> |
||
<td width=16.6667%><table cellpadding=0 cellspacing=0> |
<td width=16.6667%><table cellpadding=0 cellspacing=0> |
||
| Line 45: | Line 38: | ||
<tr align=center><td>-11</td><td bgcolor=yellow> </td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>1</td></tr> |
<tr align=center><td>-11</td><td bgcolor=yellow> </td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>1</td></tr> |
||
<tr align=center><td>-13</td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>-1</td></tr> |
<tr align=center><td>-13</td><td bgcolor=yellow>1</td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td> </td><td>-1</td></tr> |
||
</table> |
</table>}} |
||
{{Computer Talk Header}} |
{{Computer Talk Header}} |
||
| Line 109: | Line 101: | ||
q t q t</nowiki></pre></td></tr> |
q t q t</nowiki></pre></td></tr> |
||
</table> |
</table> |
||
[[Category:Knot Page]] |
|||
Revision as of 20:10, 28 August 2005
|
|
|

|
Visit 7 6's page at the Knot Server (KnotPlot driven, includes 3D interactive images!)
Visit 7 6's page at Knotilus! Visit 7 6's page at the original Knot Atlas! |
Knot presentations
| Planar diagram presentation | X1425 X3849 X5,12,6,13 X9,1,10,14 X13,11,14,10 X11,6,12,7 X7283 |
| Gauss code | -1, 7, -2, 1, -3, 6, -7, 2, -4, 5, -6, 3, -5, 4 |
| Dowker-Thistlethwaite code | 4 8 12 2 14 6 10 |
| Conway Notation | [2212] |
Three dimensional invariants
|
Four dimensional invariants
|
Polynomial invariants
Vassiliev invariants
| V2 and V3: | (1, -2) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). The squares with yellow highlighting are those on the "critical diagonals", where or , where -2 is the signature of 7 6. Nonzero entries off the critical diagonals (if any exist) are highlighted in red. |
|
| Integral Khovanov Homology
(db, data source) |
|
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
In[1]:= |
<< KnotTheory` |
Loading KnotTheory` (version of August 17, 2005, 14:44:34)... | |
In[2]:= | Crossings[Knot[7, 6]] |
Out[2]= | 7 |
In[3]:= | PD[Knot[7, 6]] |
Out[3]= | PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 12, 6, 13], X[9, 1, 10, 14], X[13, 11, 14, 10], X[11, 6, 12, 7], X[7, 2, 8, 3]] |
In[4]:= | GaussCode[Knot[7, 6]] |
Out[4]= | GaussCode[-1, 7, -2, 1, -3, 6, -7, 2, -4, 5, -6, 3, -5, 4] |
In[5]:= | BR[Knot[7, 6]] |
Out[5]= | BR[4, {-1, -1, 2, -1, -3, 2, -3}] |
In[6]:= | alex = Alexander[Knot[7, 6]][t] |
Out[6]= | -2 5 2 |
In[7]:= | Conway[Knot[7, 6]][z] |
Out[7]= | 2 4 1 + z - z |
In[8]:= | Select[AllKnots[], (alex === Alexander[#][t])&] |
Out[8]= | {Knot[7, 6], Knot[10, 133]} |
In[9]:= | {KnotDet[Knot[7, 6]], KnotSignature[Knot[7, 6]]} |
Out[9]= | {19, -2} |
In[10]:= | J=Jones[Knot[7, 6]][q] |
Out[10]= | -6 2 3 4 3 3 |
In[11]:= | Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
Out[11]= | {Knot[7, 6]} |
In[12]:= | A2Invariant[Knot[7, 6]][q] |
Out[12]= | -20 -18 -16 -12 -10 -6 -4 -2 4 -q - q + q + q + q + q - q + q + q |
In[13]:= | Kauffman[Knot[7, 6]][a, z] |
Out[13]= | 2 4 6 3 7 2 2 2 4 2 |
In[14]:= | {Vassiliev[2][Knot[7, 6]], Vassiliev[3][Knot[7, 6]]} |
Out[14]= | {0, -2} |
In[15]:= | Kh[Knot[7, 6]][q, t] |
Out[15]= | 2 2 1 1 1 2 1 2 2 |