DT (Dowker-Thistlethwaite) Codes

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

<a href=' http://homunkulus.info/ '> homunkulus </a>

<a href=' http://bambulka.info/ ' > bambulka </a>
<a href=' http://infoarena.info/ '> infoarena </a>
<a href=' http://afxbmx.info/ '> afx bmx </a>
<a href=' http://chrykne.info/ '> chrykne </a>

Links

A DT notation example, for the link L7n2

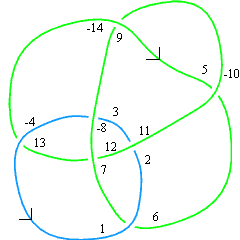
DT Codes for links are defined in a similar way (see [DollHoste]). Follow the same numbering process as for knots, except when you finish traversing one component, jump straight to the next. It is not difficult to see that there is always a choice of starting points along the components for which the resulting pairing is a pairing between odd and even numbers. (On the figure above one possible choice is indicated). Again, it is enough to only list the even numbers corresponding to $1,3,5,\ldots$; call the resulting list $\lambda$. (Above, $\lambda =(6,-8,-10,12,-14,2,-4)$). Notice that the odd indices are naturally subdivided into sublists according to the component of the link on which they lie, and this induces a subdivision of $\lambda$ into sublists. Thus with the choices made in the figure above, the DT code for the link L7n2 is $(6,-8\mid -10,12,-14,2,-4)$.

KnotTheory` knows about DT codes for links:

In[7]:=	DTCode[Link[7, NonAlternating, 2]]
Out[7]=	DTCode[{6, -8}, {-10, 12, -14, 2, -4}]

In[8]:=	MultivariableAlexander[DTCode[{6, -8}, {-10, 12, -14, 2, -4}]][t]
Out[8]=	-1 + t[1] + t[2] - t[1] t[2]

[DollHoste] ^  H. Doll and J. Hoste, A tabulation of oriented links, Mathematics of Computation 57-196 (1991) 747-761.