Invariants from Braid Theory

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

The braid length of a knot or a link $K$ is the smallest number of crossings in a braid whose closure is $K$. KnotTheory` has some braid lengths preloaded:

(For In[1] see Setup)

In[1]:= ?BraidLength BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`.

Note that the braid length of $K$ is simply the length of the minimum braid representing $K$ (see Braid Representatives):

In[2]:=	K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}
Out[2]=	{11, 11}

The braid index of a knot or a link $K$ is the smallest number of strands in a braid whose closure is $K$. KnotTheory` has some braid indices preloaded:

In[3]:= ?BraidIndex BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`.

In[4]:= BraidIndex::about The braid index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:

In[5]:=	K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}
Out[5]=	{4, 5}

In[6]:=	Show[BraidPlot[BR[K]]]
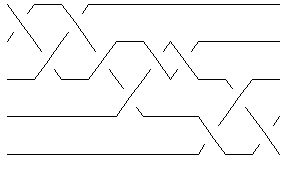
Out[6]=	-Graphics-