Invariants from Braid Theory
The braid length of a knot or a link is the smallest number of crossings in a braid whose closure is . KnotTheory` has some braid lengths preloaded:
(For In[1] see Setup)
In[2]:= ?BraidLength
BraidLength[K] returns the braid length of the knot K, if known to KnotTheory`. |
Note that the braid length of is simply the length of the minimum braid representing (see Braid Representatives):
| In[3]:= |
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]} |
| Out[3]= | {11, 11}
|
The braid index of a knot or a link is the smallest number of strands in a braid whose closure is . KnotTheory` has some braid indices preloaded:
In[4]:= ?BraidIndex
BraidIndex[K] returns the braid index of the knot K, if known to KnotTheory`. |
In[5]:= BraidIndex::about
The braid index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/. |
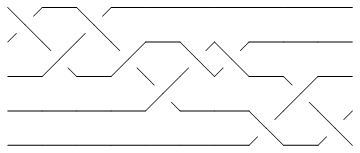
Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:
| In[6]:= |
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]} |
| Out[6]= | {4, 5}
|
| In[7]:= |
Show[BraidPlot[BR[K]]] |
| |
| Out[7]= | -Graphics- |
