Invariants from Braid Theory
From Knot Atlas
Jump to navigationJump to search
The braid length of a knot or a link is the smallest number of crossings in a braid whose closure is . KnotTheory` has some braid lengths preloaded:
(For In[1] see Setup)
| ||||
Note that the braid length of is simply the length of the minimum braid representing (see Braid Representatives):
In[3]:=
|
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}
|
Out[3]=
|
{11, 11}
|
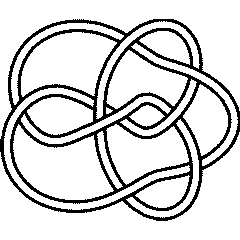 9_49 |
 10_136 |
The braid index of a knot or a link is the smallest number of strands in a braid whose closure is . KnotTheory` has some braid indices preloaded:
|
| ||||||||
Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:
In[6]:=
|
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}
|
Out[6]=
|
{4, 5}
|
In[7]:=
|
Show[BraidPlot[BR[K]]]
|
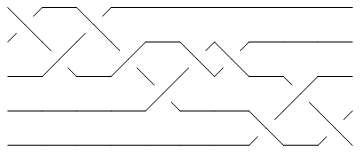
| |
Out[7]=
|
-Graphics-
|
