Cabling
From Knot Atlas
Jump to navigationJump to search
CableComponent[BR[n,js],K] returns the -th cable of the knot with the braid on strands with crossings js = {j1, j2, ...} inserted in it. It also performs the necessary number of -twists on the components of the cable to compensate for a non-zero writhe number of the original knot. Cabling knot 3_1, for instance, and inserting the braid BR[3,{1,2}], we get:
(For In[1] see Setup)
In[2]:=
|
CableComponent[n_integer, K_] := CableComponent[BR[n, {}], K];
CableComponent[BR[n_Integer, js_List], K_] :=
Module[{BC, C0, C1, C2, CC1, CS1, CS2, L, S, a, e, h, i, i1, i2, j,
j1, j2, jss, k, k1, kjs, out, out0, out1, p, p1, pos, q, r, s, ss,
t, t0, t1, t2, tj, v, w, writhe},
L = PD[K];
kjs = BR[L][[2]];
For[i1 = 1; writhe = 0, i1 <= Length[kjs], i1++,
writhe = writhe + Sign[kjs[[i1]]]];
For[i2 = 1; jss[0] = js, i2 <= n Abs[writhe], i2++,
jss[i2] =
Flatten[{jss[i2 - 1], Table[-Sign[writhe] e, {e, n - 1}]}]];
k1 = Length[jss[n Abs[writhe]]];
For[i = 1, i <= n, i++, s[i] = a[i] = i];
For[
j = 1, j <= k1, j++,
p = Select[Range[n], Abs[jss[n Abs[writhe]][[j]]] == a[#] &][[
1]];
q = Select[Range[n], a[#] == a[p] + 1 &][[1]];
If[jss[n Abs[writhe]][[j]] > 0,
K[j] = X[s[q], n + 2 j, n + 2 j - 1, s[p]],
K[j] = X[s[p], s[q], n + 2 j, n + 2 j - 1]];
s[p] = n + 2 j;
s[q] = n + 2 j - 1;
a[p]++;
a[q]--
];
BC = Table[K[d], {d, k1}];
If[Jones[L][q] === 1,
For[j1 = 1, j1 <= Length[BC], j1++,
For[i = 1, i <= n, i++, BC[[j1]] = BC[[j1]] /. s[i] :> a[i]
]];
If[BC == {}, BC = {Loop[1]}];
out1 = PD @@ BC,
For[j2 = 1, j2 <= Length[BC], j2++,
For[tj = 1, tj <= n, tj++, BC[[j2]] = BC[[j2]] /. tj :> 1[tj]]
];
p1 = Select[Range[n], # != s[#] &];
S = Select[L, MemberQ[#, 1] && MemberQ[#, 2] & ];
pos = Position[S, 1][[1, 2]];
r = Select[Table[i, {i, Length[L]}], L[[#]] == Flatten @@ S &][[
1]];
k = 0;
out0 = L /. X[a_, b_, c_, d_] :> (
++k;
Table[
X[h[i, j - 1, k], v[i, j, k], h[i, j, k], v[i - 1, j, k]],
{i, n}, {j, n}
] /. {h[i_, 0, _] :> a[i], h[i_, n, _] :> c[i]} /. If[
d - b == 1 || b - d > 1,
{v[0, j_, _] :> d[j],
v[n, j_, _] :> b[j]}, {v[0, j_, _] :> d[n + 1 - j],
v[n, j_, _] :> b[n + 1 - j]}
]
);
w = Flatten@out0[[r]];
out = PD @@ Flatten[Join @@ out0];
ss = Table[a[i], {i, n}][[p1]];
CC1 = List @@ out;
For[t0 = 1, t0 <= Length[ss], t0++,
C0[t0] = Select[w, MemberQ[#, 1[ss[[t0]]]] &];
C1[t0] =
Select[C0[t0],
Mod[Position[#, 1[ss[[t0]]]][[1, 1]], 2] == Mod[pos, 2] &];
C2[t0] =
C1[t0] /. 1[ss[[t0]]] :>
s[Select[Range[n], a[#] == ss[[t0]] &][[1]]]];
CS1 = Flatten[Table[C1[t1], {t1, Length[ss]}]];
CS2 = Flatten[Table[C2[t2], {t2, Length[ss]}]];
For[i = 1, i <= Length[CS1], i++,
CC1 = DeleteCases[CC1, CS1[[i]]]];
out1 = Union[BC, CC1, CS2];
PD @@ out1;
k = 0;
out1 =
PD @@ ( out1 /. ((# -> ++k) & /@ (List @@ Union @@ out1)))]];
|
In[3]:=
|
CableComponent[BR[3, {1, 2}], Knot[3, 1]] // DrawMorseLink
|
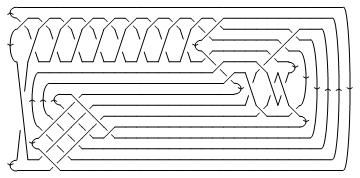
| |
Out[3]=
|
-Graphics-
|
For some special cases, we can check our result using Burau's Theorem.


