Braid Representatives: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 69: | Line 69: | ||
<!--END--> |
<!--END--> |
||
The ''minimum braid representative'' of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in {{ref|Gittings}}). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot |
The ''minimum braid representative'' of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in {{ref|Gittings}}). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot [[10_1]] has length (number of crossings) 13 and width 6 (number of strands, also see [[Invariants from Braid Theory]]): |
||
<!--$$br2 = BR[Knot[10, 1]]$$--> |
<!--$$br2 = BR[Knot[10, 1]]$$--> |
||
Revision as of 11:53, 30 August 2005
Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus for example,
In[4]:=
|
br1 = BR[2, {-1, -1, -1}];
|
In[5]:=
|
PD[br1]
|
Out[5]=
|
PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]
|
In[6]:=
|
Jones[br1][q]
|
Out[6]=
|
-4 -3 1
-q + q + -
q
|
In[7]:=
|
Mirror[br1]
|
Out[7]=
|
BR[2, {1, 1, 1}]
|
KnotTheory` has the braid representatives of some knots and links pre-loaded. Thus for example,
In[8]:=
|
BR[TorusKnot[5, 4]]
|
Out[8]=
|
BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
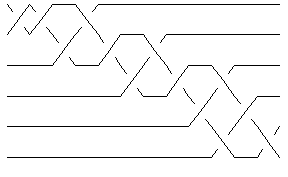
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot 10_1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):
In[9]:=
|
br2 = BR[Knot[10, 1]]
|
Out[9]=
|
BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]
|
In[11]:=
|
Show[BraidPlot[CollapseBraid[br2]]]
|
| |
Out[11]=
|
-Graphics-
|
(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)
[Gittings] ^ T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.