Naming and Enumeration: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| (53 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
<code>KnotTheory`</code> comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings {{ref|Rolfsen}}, the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see [[Further Knot Theory Software#Knotscape]]): |
|||
<code>KnotTheory`</code> comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings {{ref|Rolfsen}}, the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see [[Further Knot Theory Software#Knotscape|Knotscape]]): |
|||
<!--$Startup Note$--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
(For <tt><font color=blue>In[1]</font></tt> see [[Setup]]) |
|||
<!--END--> |
|||
{{Startup Note}} |
|||
<!--$$?Knot$$--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{| width=70% border=1 align=center |
|||
| |
|||
<font color=blue><tt>In[2]:=</tt></font><font color=red><code> ?Knot</code></font> |
|||
<!--$$?Knot$$--> |
|||
<tt>Knot[n, k] denotes the kth knot with n crossings in the Rolfsen table. Knot[11, Alternating, k] denotes the kth alternating 11-crossing knot in the Hoste-Thistlethwaite table. Knot[11, NonAlternating, k] denotes the kth non alternating 11-crossing knot in the Hoste-Thistlethwaite table.</tt> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
|} |
|||
{{HelpLine| |
|||
n = 2 | |
|||
in = <nowiki>Knot</nowiki> | |
|||
out= <nowiki>Knot[n, k] denotes the kth knot with n crossings in the Rolfsen table. Knot[n, Alternating, k] (for n between 11 and 16) denotes the kth alternating n-crossing knot in the Hoste-Thistlethwaite table. |
|||
Knot[n, NonAlternating, k] denotes the kth non alternating n-crossing knot in the Hoste-Thistlethwaite table.</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?Link$$--> |
<!--$$?Link$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{HelpLine| |
|||
{| width=70% border=1 align=center |
|||
n = 3 | |
|||
| |
|||
in = <nowiki>Link</nowiki> | |
|||
<font color=blue><tt>In[3]:=</tt></font><font color=red><code> ?Link</code></font> |
|||
out= <nowiki>Link[n, Alternating, k] denotes the kth alternating n-crossing link in the Thistlethwaite table. |
|||
Link[n, NonAlternating, k] denotes the kth non alternating n-crossing link in the Thistlethwaite table.</nowiki>}} |
|||
|} |
|||
<!--END--> |
<!--END--> |
||
{{Knot Image Pair|6_1|gif|9_46|gif}} |
|||
Thus, for example, let us verify that the knots [[6_1]] and [[9_46]] have the same Alexander polynomial: |
Thus, for example, let us verify that the knots [[6_1]] and [[9_46]] have the same Alexander polynomial: |
||
<!--$$Alexander[Knot[6, 1]][t]$$--> |
<!--$$Alexander[Knot[6, 1]][t]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
{{InOut| |
|||
<tt>In[4]:=</tt><code> Alexander[Knot[6, 1]][t]</code> |
|||
n = 4 | |
|||
in = <nowiki>Alexander[Knot[6, 1]][t]</nowiki> | |
|||
out= <nowiki> 2 |
|||
5 - - - 2 t |
|||
t</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Alexander[Knot[9, 46]][t]$$--> |
|||
<tt>Out[4]=</tt> <math>-2 t+5-\frac{2}{t}</math> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 5 | |
|||
in = <nowiki>Alexander[Knot[9, 46]][t]</nowiki> | |
|||
out= <nowiki> 2 |
|||
5 - - - 2 t |
|||
t</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
{{Knot Image|L6a4|gif}} |
|||
We can also check that the Borromean rings, [[L6a4]] in the Thistlethwaite table, is a 3-component link: |
|||
<!--$$Alexander[Knot[9, 46]][t]$$--> |
|||
<!--The lines to END were generated by WikiSplice: do not edit; see manual.--> |
|||
<tt>In[5]:=</tt><code> Alexander[Knot[9, 46]][t]</code> |
|||
<!--$$Length[Skeleton[Link[6, Alternating, 4]]]$$--> |
|||
<tt>Out[5]=</tt> <math>-2 t+5-\frac{2}{t}</math> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 6 | |
|||
in = <nowiki>Length[Skeleton[Link[6, Alternating, 4]]]</nowiki> | |
|||
out= <nowiki>3</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?AllKnots$$--> |
|||
== References== |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 7 | |
|||
in = <nowiki>AllKnots</nowiki> | |
|||
out= <nowiki>AllKnots[] return a list of all knots with up to 11 crossings. AllKnots[n_] returns a list of all knots with n crossings, up to 16. AllKnots[{n_, m_}] returns a list of all knots with between n and m crossings, and AllKnots[n_, Alternating|NonAlternating] returns all knots with n crossings of the specified type.</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?AllLinks$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 8 | |
|||
in = <nowiki>AllLinks</nowiki> | |
|||
out= <nowiki>AllLinks[] return a list of all links with up to 11 crossings. AllLinks[n_] returns a list of all links with n crossings, up to 12.</nowiki>}} |
|||
<!--END--> |
|||
Thus at the moment there are 1701936 knots and 5700 links known to <code>KnotTheory`</code>: |
|||
<!--$$Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 9 | |
|||
in = <nowiki>Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}</nowiki> | |
|||
out= <nowiki>{1701936, 5700}</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{Graphics| |
|||
n = 10 | |
|||
in = <nowiki>Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]</nowiki> | |
|||
img= Naming_and_Enumeration_Out_10.gif | |
|||
out= <nowiki>-Graphics-</nowiki>}} |
|||
<!--END--> |
|||
(Shumakovitch had noticed that this nice knot has interesting Khovanov homology; see {{ref|Shumakovitch}}). |
|||
{{Knot Image|T(5,3)|jpg}} |
|||
In addition to the tables, KnotTheory` also knows about torus knots: |
|||
<!--$$?TorusKnot$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 11 | |
|||
in = <nowiki>TorusKnot</nowiki> | |
|||
out= <nowiki>TorusKnot[m, n] represents the (m,n) torus knot.</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?TorusKnots$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 12 | |
|||
in = <nowiki>TorusKnots</nowiki> | |
|||
out= <nowiki>TorusKnots[n_] returns a list of all torus knots with up to n crossings.</nowiki>}} |
|||
<!--END--> |
|||
For example, the torus knots [[T(5,3)]] and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant <math>V_3</math>): |
|||
<!--$$Crossings /@ {TorusKnot[5, 3], TorusKnot[3, 5]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 13 | |
|||
in = <nowiki>Crossings /@ {TorusKnot[5, 3], TorusKnot[3, 5]}</nowiki> | |
|||
out= <nowiki>{10, 12}</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Vassiliev[3] /@ {TorusKnot[5, 3], TorusKnot[3, 5]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 14 | |
|||
in = <nowiki>Vassiliev[3] /@ {TorusKnot[5, 3], TorusKnot[3, 5]}</nowiki> | |
|||
out= <nowiki>{20, 20}</nowiki>}} |
|||
<!--END--> |
|||
KnotTheory` knows how to plot torus knots; see [[Drawing with TubePlot]]. |
|||
You can also use the function Knot to parse certain string representations of named knots: |
|||
<!--$$Knot /@ {"K11a14", "11a_14", "L8a1", "T(3,5)"}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 15 | |
|||
in = <nowiki>Knot /@ {"K11a14", "11a_14", "L8a1", "T(3,5)"}</nowiki> | |
|||
out= <nowiki>{Knot[11, Alternating, 14], If[11 a <= 10 && |
|||
14 <= NumberOfKnots[11 a, Alternating] + |
|||
NumberOfKnots[11 a, NonAlternating], |
|||
Knot @@ KnotTheory`Naming`s$3008], Link[8, Alternating, 1], |
|||
TorusKnot[3, 5]}</nowiki>}} |
|||
<!--END--> |
|||
In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas. |
|||
<!--$$NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 16 | |
|||
in = <nowiki>NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}</nowiki> | |
|||
out= <nowiki>{K11a14, T(3,5)}</nowiki>}} |
|||
<!--END--> |
|||
==References== |
|||
{{note|Rolfsen}} D. Rolfsen, ''Knots and Links'', Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976. |
|||
{{note|Shumakovitch}} A. Shumakovitch, ''Torsion of the Khovanov Homology'', [http://front.math.ucdavis.edu/math.GT/0405474 arXiv:math.GT/0405474]. |
|||
{{note|Rolfsen}} D. Rolfsen, ''Knots and Links'', Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976. |
|||
Latest revision as of 17:18, 21 February 2013
KnotTheory` comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings [Rolfsen], the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see Knotscape):
(For In[1] see Setup)
| ||||
| ||||
 6_1 |
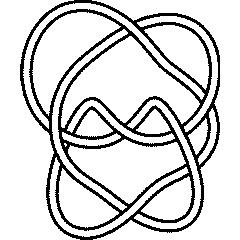 9_46 |
Thus, for example, let us verify that the knots 6_1 and 9_46 have the same Alexander polynomial:
In[4]:=
|
Alexander[Knot[6, 1]][t]
|
Out[4]=
|
2
5 - - - 2 t
t
|
In[5]:=
|
Alexander[Knot[9, 46]][t]
|
Out[5]=
|
2
5 - - - 2 t
t
|
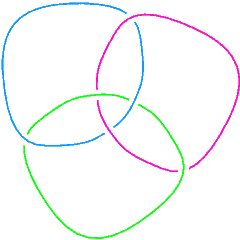 L6a4 |
We can also check that the Borromean rings, L6a4 in the Thistlethwaite table, is a 3-component link:
In[6]:=
|
Length[Skeleton[Link[6, Alternating, 4]]]
|
Out[6]=
|
3
|
| ||||
| ||||
Thus at the moment there are 1701936 knots and 5700 links known to KnotTheory`:
In[9]:=
|
Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}
|
Out[9]=
|
{1701936, 5700}
|
In[10]:=
|
Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]
|
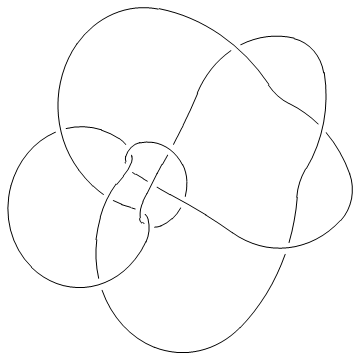
| |
Out[10]=
|
-Graphics-
|
(Shumakovitch had noticed that this nice knot has interesting Khovanov homology; see [Shumakovitch]).
 T(5,3) |
In addition to the tables, KnotTheory` also knows about torus knots:
| ||||
| ||||
For example, the torus knots T(5,3) and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant [math]\displaystyle{ V_3 }[/math]):
In[13]:=
|
Crossings /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
|
Out[13]=
|
{10, 12}
|
In[14]:=
|
Vassiliev[3] /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
|
Out[14]=
|
{20, 20}
|
KnotTheory` knows how to plot torus knots; see Drawing with TubePlot.
You can also use the function Knot to parse certain string representations of named knots:
In[15]:=
|
Knot /@ {"K11a14", "11a_14", "L8a1", "T(3,5)"}
|
Out[15]=
|
{Knot[11, Alternating, 14], If[11 a <= 10 &&
14 <= NumberOfKnots[11 a, Alternating] +
NumberOfKnots[11 a, NonAlternating],
Knot @@ KnotTheory`Naming`s$3008], Link[8, Alternating, 1],
TorusKnot[3, 5]}
|
In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas.
In[16]:=
|
NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}
|
Out[16]=
|
{K11a14, T(3,5)}
|
References
[Rolfsen] ^ D. Rolfsen, Knots and Links, Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976.
[Shumakovitch] ^ A. Shumakovitch, Torsion of the Khovanov Homology, arXiv:math.GT/0405474.