Structure and Operations: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
{{Startup Note}} |
{{Startup Note}} |
||
<!--$$?Crossings$$--> |
<!--$$?Crossings$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 2 | |
|||
in = <nowiki>Crossings</nowiki> | |
|||
out= <nowiki>Crossings[L] returns the number of crossings of a knot/link L (in its given presentation).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?PositiveCrossings$$--> |
<!--$$?PositiveCrossings$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 3 | |
|||
in = <nowiki>PositiveCrossings</nowiki> | |
|||
out= <nowiki>PositiveCrossings[L] returns the number of positive (right handed) crossings in a knot/link L (in its given presentation).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?NegativeCrossings$$--> |
<!--$$?NegativeCrossings$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 4 | |
|||
in = <nowiki>NegativeCrossings</nowiki> | |
|||
out= <nowiki>NegativeCrossings[L] returns the number of negative (left handed) crossings in a knot/link L (in its given presentation).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
Thus here's one tautology and one easy example: |
Thus here's one tautology and one easy example: |
||
<!--$$Crossings /@ {Knot[0, 1], TorusKnot[11,10]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 5 | |
|||
in = <nowiki>Crossings /@ {Knot[0, 1], TorusKnot[11,10]}</nowiki> | |
|||
out= <nowiki>{0, 99}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
And another easy example: |
And another easy example: |
||
<!--$$K=Knot[6, 2]; {PositiveCrossings[K], NegativeCrossings[K]}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 6 | |
|||
in = <nowiki>K=Knot[6, 2]; {PositiveCrossings[K], NegativeCrossings[K]}</nowiki> | |
|||
out= <nowiki>{2, 4}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?PositiveQ$$--> |
<!--$$?PositiveQ$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 7 | |
|||
in = <nowiki>PositiveQ</nowiki> | |
|||
out= <nowiki>PositiveQ[xing] returns True if xing is a positive (right handed) crossing and False if it is negative (left handed).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?NegativeQ |
<!--$$?NegativeQ$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 8 | |
|||
in = <nowiki>NegativeQ</nowiki> | |
|||
out= <nowiki>NegativeQ[xing] returns True if xing is a negative (left handed) crossing and False if it is positive (right handed).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
| Line 29: | Line 66: | ||
<!--$$PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}$$--> |
<!--$$PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 9 | |
|||
in = <nowiki>PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}</nowiki> | |
|||
out= <nowiki>{False, True, True, True}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?ConnectedSum |
<!--$$?ConnectedSum$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 10 | |
|||
in = <nowiki>ConnectedSum</nowiki> | |
|||
out= <nowiki>ConnectedSum[K1, K2] represents the connected sum of the knots K1 and K2 (ConnectedSum may not work with links).</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
The connected sum <math>K=4_1\#4_1</math> of the knot [[4_1]] with itself has 8 crossings (unsurprisingly): |
The connected sum <math>K=4_1\#4_1</math> of the knot [[4_1]] with itself has 8 crossings (unsurprisingly): |
||
<!--$$ |
<!--$$K = ConnectedSum[Knot[4,1], Knot[4,1]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 11 | |
|||
in = <nowiki>K = ConnectedSum[Knot[4,1], Knot[4,1]]</nowiki> | |
|||
out= <nowiki>ConnectedSum[Knot[4, 1], Knot[4, 1]]</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$Crossings[K]$$--> |
<!--$$Crossings[K]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 12 | |
|||
in = <nowiki>Crossings[K]</nowiki> | |
|||
out= <nowiki>8</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
It is also nice to know that, as expected, the Jones polynomial of <math>K</math> is the square of the Jones polynomial of [[4_1]]: |
It is also nice to know that, as expected, the Jones polynomial of <math>K</math> is the square of the Jones polynomial of [[4_1]]: |
||
<!--$$Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]$$--> |
<!--$$Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 13 | |
|||
in = <nowiki>Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]</nowiki> | |
|||
out= <nowiki>True</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
{{Knot Image Pair|4_1|gif|8_9|gif}} |
|||
It is less nice to know that the Jones polynomial cannot tell <math>K</math> apart from the knot [[8_9]]: |
It is less nice to know that the Jones polynomial cannot tell <math>K</math> apart from the knot [[8_9]]: |
||
<!--$$Jones[K][q] == Jones[Knot[8,9]][q]$$--> |
<!--$$Jones[K][q] == Jones[Knot[8,9]][q]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 14 | |
|||
in = <nowiki>Jones[K][q] == Jones[Knot[8,9]][q]</nowiki> | |
|||
out= <nowiki>True</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
| Line 56: | Line 124: | ||
<!--$${Alexander[K][t], Alexander[Knot[8,9]][t]}$$--> |
<!--$${Alexander[K][t], Alexander[Knot[8,9]][t]}$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 15 | |
|||
in = <nowiki>{Alexander[K][t], Alexander[Knot[8,9]][t]}</nowiki> | |
|||
out= <nowiki> -2 6 2 -3 3 5 2 3 |
|||
{11 + t - - - 6 t + t , 7 - t + -- - - - 5 t + 3 t - t } |
|||
t 2 t |
|||
t</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
Latest revision as of 17:20, 21 February 2013
(For In[1] see Setup)
| ||||
| ||||
| ||||
Thus here's one tautology and one easy example:
In[5]:=
|
Crossings /@ {Knot[0, 1], TorusKnot[11,10]}
|
Out[5]=
|
{0, 99}
|
And another easy example:
In[6]:=
|
K=Knot[6, 2]; {PositiveCrossings[K], NegativeCrossings[K]}
|
Out[6]=
|
{2, 4}
|
| ||||
| ||||
For example,
In[9]:=
|
PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}
|
Out[9]=
|
{False, True, True, True}
|
| ||||
The connected sum [math]\displaystyle{ K=4_1\#4_1 }[/math] of the knot 4_1 with itself has 8 crossings (unsurprisingly):
In[11]:=
|
K = ConnectedSum[Knot[4,1], Knot[4,1]]
|
Out[11]=
|
ConnectedSum[Knot[4, 1], Knot[4, 1]]
|
In[12]:=
|
Crossings[K]
|
Out[12]=
|
8
|
It is also nice to know that, as expected, the Jones polynomial of [math]\displaystyle{ K }[/math] is the square of the Jones polynomial of 4_1:
In[13]:=
|
Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]
|
Out[13]=
|
True
|
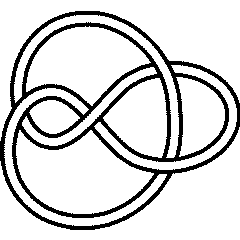 4_1 |
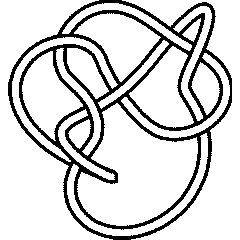 8_9 |
It is less nice to know that the Jones polynomial cannot tell [math]\displaystyle{ K }[/math] apart from the knot 8_9:
In[14]:=
|
Jones[K][q] == Jones[Knot[8,9]][q]
|
Out[14]=
|
True
|
But [math]\displaystyle{ K=4_1\#4_1 }[/math] isn't equivalent to 8_9; indeed, their Alexander polynomials are different:
In[15]:=
|
{Alexander[K][t], Alexander[Knot[8,9]][t]}
|
Out[15]=
|
-2 6 2 -3 3 5 2 3
{11 + t - - - 6 t + t , 7 - t + -- - - - 5 t + 3 t - t }
t 2 t
t
|