Burau's Theorem: Difference between revisions
(New page: {{Manual TOC Sidebar}} An interesting property of the Alexander polynomial related to cables is Burau's theorem which says the following: If we take the n-th cable of a knot from the Knot...) |
No edit summary |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
An interesting property of the Alexander polynomial related to cables is Burau's theorem which says the following: If we take the n-th cable of a knot from the Knot Atlas and insert in it a braid with 1/n of a full twist, the Alexander polynomial of the result with respect to t is the same as the Alexander polynomial of the original knot with respect to t< |
An interesting property of the Alexander polynomial related to cables is Burau's theorem which says the following: If we take the <math>n</math>-th cable of a knot from the Knot Atlas and insert in it a braid with <math>1/n</math> of a full twist, the Alexander polynomial of the result with respect to <math>t</math> is the same as the Alexander polynomial of the original knot with respect to <math>t^n</math>. This can only be seen if we take into consideration the writhe <math>w</math> of the knot and add the appropriate number of twists (<math>nw(1/n)=w</math> full twists) in the direction opposite to the sign of the writhe. We can test the theorem using the program [[Cabling|CableComponent]] and performing the above operation on knot [[K11n152]], for example. |
||
This can only be seen if we take into consideration the writhe of the knot and add the appropriate number of twists (n(writhe)(1/n)=writhe full twists, where the writhe is nonzero) in the direction opposite to the sign of the writhe. |
|||
We can test the theorem using the program [[Cabling|CableComponent]] and performing the above operation on knot [[K11n152]], for example. |
|||
{{Startup Note}} |
{{Startup Note}} |
||
<!--$$Import["http://katlas.org/w/index.php?title=CableComponent.m&action=raw"];$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{In| |
|||
n = 2 | |
|||
in = <nowiki>Import["http://katlas.org/w/index.php?title=CableComponent.m&action=raw"];</nowiki>}} |
|||
<!--END--> |
|||
<!--$$(cc = CableComponent[BR[6, {1, 2, 3, 4, 5}], |
<!--$$(cc = CableComponent[BR[6, {1, 2, 3, 4, 5}], |
||
| Line 12: | Line 17: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 3 | |
||
in = <nowiki>(cc = CableComponent[BR[6, {1, 2, 3, 4, 5}], |
in = <nowiki>(cc = CableComponent[BR[6, {1, 2, 3, 4, 5}], |
||
K = Mirror[Knot[11, NonAlternating, 52]]]) // DrawMorseLink |
K = Mirror[Knot[11, NonAlternating, 52]]]) // DrawMorseLink |
||
</nowiki> | |
</nowiki> | |
||
img= |
img= Buraus_Theorem_Out_3.gif | |
||
out= <nowiki>-Graphics-</nowiki>}} |
out= <nowiki>-Graphics-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 23: | Line 28: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 4 | |
||
in = <nowiki>Alexander[#][t] & /@ {cc, K}</nowiki> | |
in = <nowiki>Alexander[#][t] & /@ {cc, K}</nowiki> | |
||
out= <nowiki> -18 6 14 6 12 18 |
out= <nowiki> -18 6 14 6 12 18 |
||
Latest revision as of 14:07, 20 October 2013
An interesting property of the Alexander polynomial related to cables is Burau's theorem which says the following: If we take the -th cable of a knot from the Knot Atlas and insert in it a braid with of a full twist, the Alexander polynomial of the result with respect to is the same as the Alexander polynomial of the original knot with respect to . This can only be seen if we take into consideration the writhe of the knot and add the appropriate number of twists ( full twists) in the direction opposite to the sign of the writhe. We can test the theorem using the program CableComponent and performing the above operation on knot K11n152, for example.
(For In[1] see Setup)
In[2]:=
|
Import["http://katlas.org/w/index.php?title=CableComponent.m&action=raw"];
|
In[3]:=
|
(cc = CableComponent[BR[6, {1, 2, 3, 4, 5}],
K = Mirror[Knot[11, NonAlternating, 52]]]) // DrawMorseLink
|
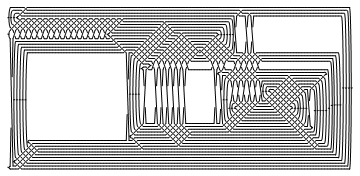
| |
Out[3]=
|
-Graphics-
|
It is not immediately clear from the diagram that this is the expected result but we can see that the Alexander polynomial relation holds:
In[4]:=
|
Alexander[#][t] & /@ {cc, K}
|
Out[4]=
|
-18 6 14 6 12 18
{-17 + t - --- + -- + 14 t - 6 t + t ,
12 6
t t
-3 6 14 2 3
-17 + t - -- + -- + 14 t - 6 t + t }
2 t
t
|





