Braid Representatives: Difference between revisions
No edit summary |
No edit summary |
||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 8: | Line 8: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpAndAbout| |
{{HelpAndAbout| |
||
n = |
n = 2 | |
||
n1 = |
n1 = 3 | |
||
in = <nowiki>BR</nowiki> | |
in = <nowiki>BR</nowiki> | |
||
out= <nowiki>BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": |
out= <nowiki>BR stands for Braid Representative. BR[k, l] represents a braid on k strands with crossings l={i1, i2, ...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": |
||
BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot.</nowiki> | |
|||
about= <nowiki>The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. |
about= <nowiki>The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. |
||
Vogel's algorithm was implemented by Dan Carney in the summer of 2005 at the University of Toronto.</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
| Line 18: | Line 20: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 4 | |
||
in = <nowiki>Mirror</nowiki> | |
in = <nowiki>Mirror</nowiki> | |
||
out= <nowiki>Mirror[br] return the mirror braid of br.</nowiki>}} |
out= <nowiki>Mirror[br] return the mirror braid of br.</nowiki>}} |
||
| Line 28: | Line 30: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{In| |
{{In| |
||
n = |
n = 5 | |
||
in = <nowiki>br1 = BR[2, {-1, -1, -1}];</nowiki>}} |
in = <nowiki>br1 = BR[2, {-1, -1, -1}];</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 36: | Line 38: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 6 | |
||
in = <nowiki>PD[br1]</nowiki> | |
in = <nowiki>PD[br1]</nowiki> | |
||
out= <nowiki>PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]</nowiki>}} |
out= <nowiki>PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]</nowiki>}} |
||
| Line 44: | Line 46: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 7 | |
||
in = <nowiki>Jones[br1][q]</nowiki> | |
in = <nowiki>Jones[br1][q]</nowiki> | |
||
out= <nowiki> -4 -3 1 |
out= <nowiki> -4 -3 1 |
||
| Line 54: | Line 56: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 8 | |
||
in = <nowiki>Mirror[br1]</nowiki> | |
in = <nowiki>Mirror[br1]</nowiki> | |
||
out= <nowiki>BR[2, {1, 1, 1}]</nowiki>}} |
out= <nowiki>BR[2, {1, 1, 1}]</nowiki>}} |
||
| Line 66: | Line 68: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 9 | |
||
in = <nowiki>BR[TorusKnot[5, 4]]</nowiki> | |
in = <nowiki>BR[TorusKnot[5, 4]]</nowiki> | |
||
out= <nowiki>BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]</nowiki>}} |
out= <nowiki>BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]</nowiki>}} |
||
| Line 74: | Line 76: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 10 | |
||
in = <nowiki>BR[Knot[11, Alternating, 362]]</nowiki> | |
in = <nowiki>BR[Knot[11, Alternating, 362]]</nowiki> | |
||
out= <nowiki>BR[10, {1, 2, -3, -4, 5, 6, 5, 4, 3, -2, -1, -4, 3, -2, -4, 3, 5, 4, |
out= <nowiki>BR[10, {1, 2, -3, -4, 5, 6, 5, 4, 3, -2, -1, -4, 3, -2, -4, 3, 5, 4, |
||
| Line 92: | Line 94: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 11 | |
||
in = <nowiki>br2 = BR[Knot[10, 1]]</nowiki> | |
in = <nowiki>br2 = BR[Knot[10, 1]]</nowiki> | |
||
out= <nowiki>BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]</nowiki>}} |
out= <nowiki>BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]</nowiki>}} |
||
| Line 102: | Line 104: | ||
n = 12 | |
n = 12 | |
||
in = <nowiki>Show[BraidPlot[CollapseBraid[br2]]]</nowiki> | |
in = <nowiki>Show[BraidPlot[CollapseBraid[br2]]]</nowiki> | |
||
img= |
img= Braid_Representatives_Out_12.gif | |
||
out= <nowiki>-Graphics-</nowiki>}} |
out= <nowiki>-Graphics-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 111: | Line 113: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 13 | |
||
in = <nowiki>Show[BraidPlot[CollapseBraid[BR[Knot[5, 2]]]]]</nowiki> | |
in = <nowiki>Show[BraidPlot[CollapseBraid[BR[Knot[5, 2]]]]]</nowiki> | |
||
img= Braid_Representatives_Out_13.gif | |
img= Braid_Representatives_Out_13.gif | |
||
| Line 122: | Line 124: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 14 | |
||
in = <nowiki>pd = PD[Knot[5, 2]]</nowiki> | |
in = <nowiki>pd = PD[Knot[5, 2]]</nowiki> | |
||
out= <nowiki>PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 10, 6, 1], X[9, 6, 10, 7], |
out= <nowiki>PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 10, 6, 1], X[9, 6, 10, 7], |
||
| Line 134: | Line 136: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
{{Graphics| |
||
n = |
n = 15 | |
||
in = <nowiki>Show[BraidPlot[CollapseBraid[BR[pd]]]]</nowiki> | |
in = <nowiki>Show[BraidPlot[CollapseBraid[BR[pd]]]]</nowiki> | |
||
img= |
img= Braid_Representatives_Out_15.gif | |
||
out= <nowiki>-Graphics-</nowiki>}} |
out= <nowiki>-Graphics-</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
Latest revision as of 17:11, 21 February 2013
Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus for example,
In[5]:=
|
br1 = BR[2, {-1, -1, -1}];
|
In[6]:=
|
PD[br1]
|
Out[6]=
|
PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]
|
In[7]:=
|
Jones[br1][q]
|
Out[7]=
|
-4 -3 1
-q + q + -
q
|
In[8]:=
|
Mirror[br1]
|
Out[8]=
|
BR[2, {1, 1, 1}]
|
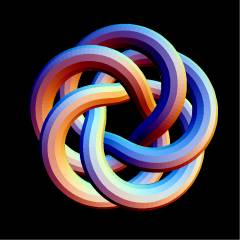 T(5,4) |
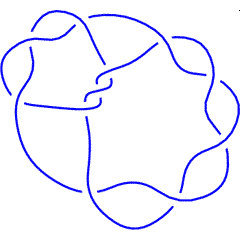 K11a362 |
KnotTheory` has the braid representatives of some knots and links pre-loaded, and for all other knots and links it will find a braid representative using Vogel's algorithm. Thus for example,
In[9]:=
|
BR[TorusKnot[5, 4]]
|
Out[9]=
|
BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
In[10]:=
|
BR[Knot[11, Alternating, 362]]
|
Out[10]=
|
BR[10, {1, 2, -3, -4, 5, 6, 5, 4, 3, -2, -1, -4, 3, -2, -4, 3, 5, 4,
-6, 7, -6, 5, 8, 7, 6, 5, -4, -3, 2, 5, -6, 9, -8, 7, -6, 5, 4, -3,
5, 6, 5, 4, 5, -7, 8, -7, 6, 5, -9, -8, -7}]
|
(As we see, Vogel's algorithm sometimes produces scary results. A 51-crossings braid representative for an 11-crossing knot, in the case of K11a362).
 10_1 |
 5_2 |
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot 10_1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):
In[11]:=
|
br2 = BR[Knot[10, 1]]
|
Out[11]=
|
BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]
|
In[12]:=
|
Show[BraidPlot[CollapseBraid[br2]]]
|
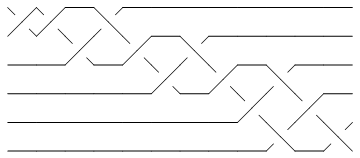
| |
Out[12]=
|
-Graphics-
|
Already for the knot 5_2 the minimum braid is shorter than the braid produced by Vogel's algorithm. Indeed, the minimum braid is
In[13]:=
|
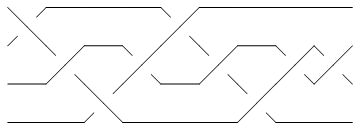
Show[BraidPlot[CollapseBraid[BR[Knot[5, 2]]]]]
|
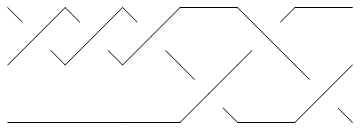
| |
Out[13]=
|
-Graphics-
|
To force KnotTheory` to run Vogel's algorithm on 5_2, we first convert it to its PD form,
In[14]:=
|
pd = PD[Knot[5, 2]]
|
Out[14]=
|
PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 10, 6, 1], X[9, 6, 10, 7],
X[7, 2, 8, 3]]
|
and only then run BR:
In[15]:=
|
Show[BraidPlot[CollapseBraid[BR[pd]]]]
|
| |
Out[15]=
|
-Graphics-
|
(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)
[Gittings] ^ T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.