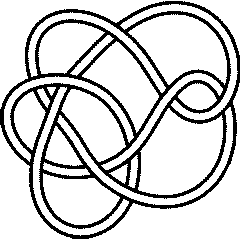The Determinant and the Signature: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 71: | Line 71: | ||
So the "first" knots that are not <math>k</math>-colourable for any <math>k</math> are [[10_124]] and [[10_153]]. |
So the "first" knots that are not <math>k</math>-colourable for any <math>k</math> are [[10_124]] and [[10_153]]. |
||
{{Knot Image|10_153|gif}} |
|||
Revision as of 08:15, 2 September 2005
(For In[1] see Setup)
| ||||
| ||||
Thus, for example, the knots 5_1 and 10_132 have the same determinant (and even the same Alexander and Jones polynomials), but different signatures:
In[3]:=
|
KnotDet /@ {Knot[5, 1], Knot[10, 132]}
|
Out[3]=
|
{5, 5}
|
In[4]:=
|
{
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}),
Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]})
}
|
Out[4]=
|
{True, True}
|
In[5]:=
|
KnotSignature /@ {Knot[5, 1], Knot[10, 132]}
|
Out[5]=
|
{-4, 0}
|
In August 2005 somebody emailed Dror a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is . So on September 2nd Dror typed
In[6]:=
|
Select[AllKnots[], Abs[KnotDet[#]] == 1 &]
|
Out[6]=
|
{Knot[0, 1], Knot[10, 124], Knot[10, 153],
Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42],
Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}
|
So the "first" knots that are not -colourable for any are 10_124 and 10_153.
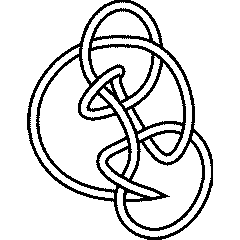 10_153 |