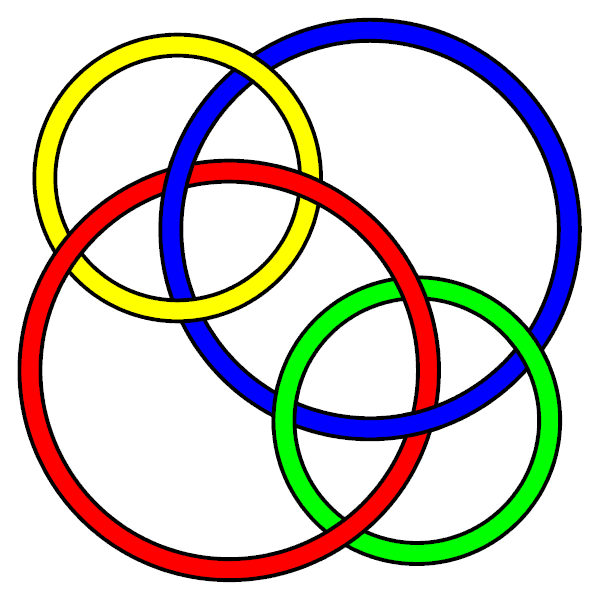User talk:Drorbn

Hello again, Mr. Bar Natan. Thank you for helping me out with my problem. Dr. Conant said that your two examples were similar to his. Anyway, Dr. Conant told me that he became interested in knot theory because you showed up at a presentation he attended. I hope your knot theory career remains a successful one.

Strongbad, 2006-03-14 09:58-05:00

Site - very comprehensive and meticulous from all points of view, it�s good! Just excellent website, I'm sure!

prozac | buy prozac online | ambien cr | prozac overdose

Borromean chain-mail knot?

Which knot number is the "Borromean chain mail" knot? It's not L10a169, but I'm having difficulty determining which it actually is... AnonMoos 15:49, 27 Mar 2006 (EST)

Can't tell without a bit of a search, but I'm running out of time for today... --Drorbn 17:42, 27 Mar 2006 (EST)

Ok, it is L10n107. --Drorbn 21:46, 27 Mar 2006 (EST)

Ok, thanks (of course, I just assumed it was alternating without examining it, sorry). AnonMoos 23:40, 28 Mar 2006 (EST)

Linear decorative knot

Sorry to keep bothering you, but I was looking at the simplest Celtic or pseudo-Celtic linear decorative knot, and it seems to be a real 8-crossing two-loop alternating link (when you shake it, it definitely does not fall apart), but I'm having difficulty relating it to any of the visual depictions on page The Thistlethwaite Link Table L8a1-L8a21... AnonMoos 12:24, 2 Apr 2006 (EDT)

Cool! It is the mirror image of L8a8, and it is not obvious to see that. In fact, I had to run the program KnotTheory` and see that the two have the same (i.e., opposite) invariants.

The Knot Atlas does not distinguish a knot from its mirror, so the picture should go on the L8a8 page. --Drorbn 16:13, 2 Apr 2006 (EDT)

Ok, thanks. It seems that there isn't really currently any program which will take a quasi-arbitrary input diagram and automatically report back "That's link #782 on the list." AnonMoos 22:19, 3 Apr 2006 (EDT)

Another linear decorative knot

I'm having difficulty in relating this to any of the list of alternating 10-crossing two-loop links, thanks... AnonMoos 21:42, 20 Jun 2006 (EDT)

Ouch! That was some strugle for me too, and it underlines the fact that my/our tools for doing such searches are not good enough. First I scanned the link table by hand and found nothing. Then I've quickly entered by hand a DTCode for your link, and it came out to be DTCode[{6, 12, 20, 16, 18}, {2, 4, 10, 8, 14}]. Then I computed the Jones polynomial of that and compared it with the Jones polynomials of all 10 crossings alternating links. Only two links differed from ours by a power of $q$ - L10a31 and L10a101. Of these the first gets ruled out immediately. The second seemed possible, but just to be sure I computed its Multivariable Alexander polynomial and found that it was complete different than the MVA of your link. After flipping the orientation of one of the components of your link so as to get DTCode[{6, 20, 12, 16, 14}, {2, 18, 8, 10, 4}], everything is well.

So the answer is L10a101.

--Drorbn 10:30, 23 Jun 2006 (EDT)

Sorry if I was imposing an excessively fatiguing task on you, but I kind of like to correlate the decorative and/or symbolic motifs. Anyway, I'm already more or less approaching the limits of what has been done in that area with 11 or fewer crossings...

I did download Knotscape, and booted Linux to run it, and that helped me identify Image:Vodicka-3pointed-knot.gif as 10_75, but it seems that nothing except getting into the nitty gritty of the mathematics helps with multi-loop knots (links)...

If two-loop links which are actually inherently symmetrical between the two loops (as L10a101 seems to be) were always portrayed symmetically, that would be helpful. AnonMoos 22:16, 27 Jun 2006 (EDT)

Here's one

http://commons.wikimedia.org/wiki/Image:Gateknot.jpg AnonMoos 11:00, 6 Jul 2006 (EDT)

Almost certainly it's either K11n34 or K11n42 and my hunch is that it's the former. It's a bit embarassing but the tools I have (and that are available through the Knot Atlas) cannot tell these two knot apart computationaly. So at the moment, to decide which of the two this is, one would have to draw and play with the drawings, or to tie a piece of string and play with it. --Drorbn 21:00, 11 Jul 2006 (EDT)

Thanks... AnonMoos 11:11, 15 Jul 2006 (EDT)

Me again

I'm having a hard time mentally correlating Image:Suchy-Vaud-Switz-COA.gif with L6n1, but there don't seem to be a lot of other choices for non-alternating six-crossing three-loop links. If it comes down to it, I'm not absolutely 100% sure that Image:Valknut-Symbol-3linkchain-closed.png is L6a5 either (I thought so for a long time, but now that I look at all the six-crossing three-loop links side-by-side, my certainty is fading a little). Thanks... AnonMoos 13:18, 20 Feb 2007 (EST)

Image:Suchy-Vaud-Switz-COA.gif does seem like L6n1, to me. Take for example the upper ring (that is, the ring closest to the teeth of the key) in the "white link blue background" portion of the image, and spin it half way around a vertical axis in the plane of the screen. I believe you'll get L6n1.

It seems to me that Image:Valknut-Symbol-3linkchain-closed.png is indeed mis-identified; it should be L6n1 as well. --Drorbn 21:57, 22 Feb 2007 (EST)

Thanks -- I moved to the L6n1 Further Notes and Views page accordingly. AnonMoos 19:14, 24 Feb 2007 (EST)

9 crossings?

I'm having problems with this one -- it doesn't closely visually resemble any of the 9-crossing knots shown in the table, and all Knotscape will tell me is "Non-prime Dowker code". AnonMoos 15:43, 2 Mar 2007 (EST)

For indeed it is a non-prime knot - it is the "connected sum" of three 3 1's. Knots have a "factorization into primes" theorem, much like the factorization into primes theorem of number theory. So in some sense, "decomposable" knots are not interesting, because if you know all about prime knots you also know all about decomposable knots as well. Hence decomposable knots are not listed on the Knot Atlas. --Drorbn 16:03, 2 Mar 2007 (EST)

OK, sorry if I'm embarrasingly ignorant of some of the basics, but I'm more interested in the decorative geometry aspects than in pure mathematical topology. Feel free to delete the image if it has no use here... AnonMoos 18:31, 2 Mar 2007 (EST)

Why delete? It's nice to have, if only just on my talk page... --Drorbn 18:41, 2 Mar 2007 (EST)

---

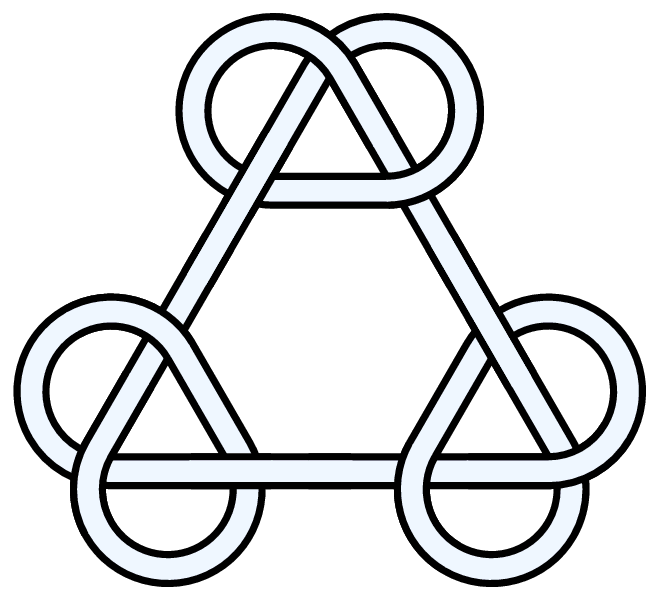
Here's another visual variant from my efforts on decorative knots... Maybe these could be included on the 3_1 page? AnonMoos 21:56, 4 May 2007 (EDT)

(Hopefully) Final question on the decorative knots

I was a little reluctant to ask you this before, since you were having such an arduous time identifying complex links, but if you could pin down this particular one (which comes in several decorative variations, and is the next step up from the symmetrical representation of L8a8), then it would pretty much complete the decorative knots series (at least with respect to knots and links with 11 or fewer crossings). This looks like it has 11 crossings, but I have reason to suspect that it may be reducible to a form with only 10 crossings..

See The_Multivariable_Alexander_Polynomial#Detecting_a_Link_Using_the_Multivariable_Alexander_Polynomial. --Drorbn 16:16, 3 May 2007 (EDT)

Thanks (hope it wasn't too strenuous an effort!). I only played with Mathematica briefly a number of years ago, and don't have access to it now... AnonMoos 21:58, 4 May 2007 (EDT)