Brunnian link: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
The name Brunnian is after Hermann Brunn, whose 1892 article ''Über Verkettung'' included examples of such links. |
The name Brunnian is after Hermann Brunn, whose 1892 article ''Über Verkettung'' included examples of such links. |
||
The best-known and simplest possible Brunnian link is the [[L6a4|Borromean rings]], a link of three unknots. (This is also the only Brunnian link |
The best-known and simplest possible Brunnian link is the [[L6a4|Borromean rings]], a link of three unknots. (This is also the only Brunnian link with less than 10 crossings, and the only symmetrical Brunnian link with less than 12 crossings.) However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: |
||
<gallery> |
<gallery> |
||
| Line 21: | Line 21: | ||
==See also== |
==See also== |
||
*[[L10a140]] |
|||
*[[L11a434]] |
|||
*[[L11n436]] |
|||
*[["Rubberband" Brunnian Links]] |
*[["Rubberband" Brunnian Links]] |
||
==Further reading== |
|||
T.Kanenobu, Hyperbolic links with Brunnian properties. J. Math. Soc. Japan. Vol 38 No. 2, (1986) 295--308. |
T.Kanenobu, Hyperbolic links with Brunnian properties. J. Math. Soc. Japan. Vol 38 No. 2, (1986) 295--308. |
||
Latest revision as of 13:28, 29 April 2013
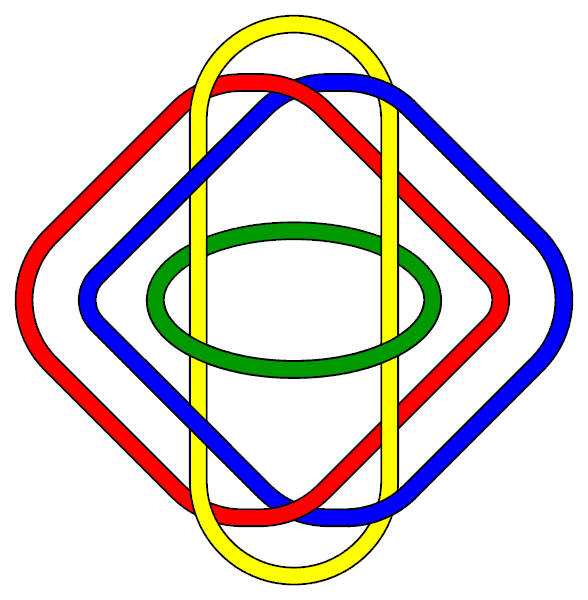
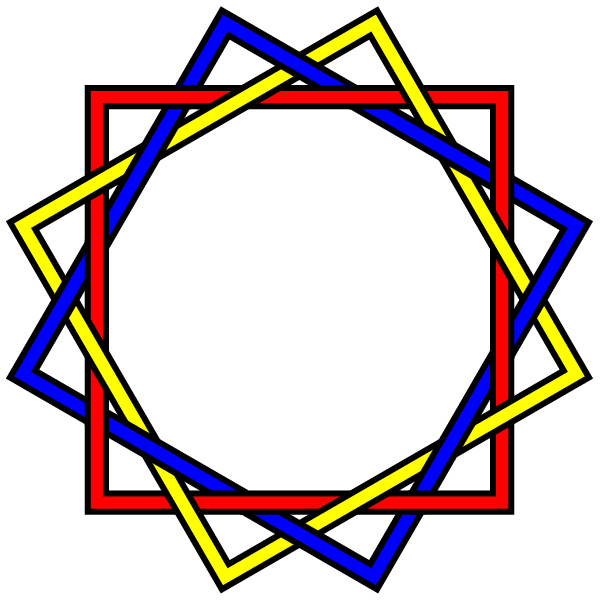
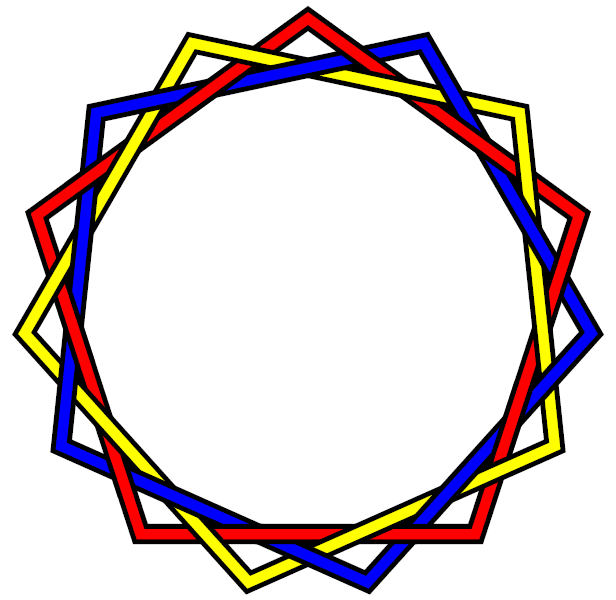
A Brunnian link is a nontrivial link which becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops (so that there is no Hopf link between any two loops).
The name Brunnian is after Hermann Brunn, whose 1892 article Über Verkettung included examples of such links.
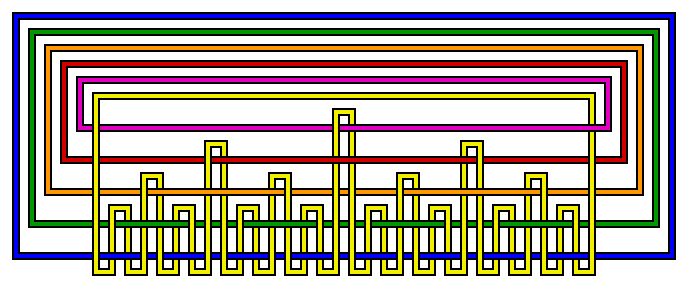
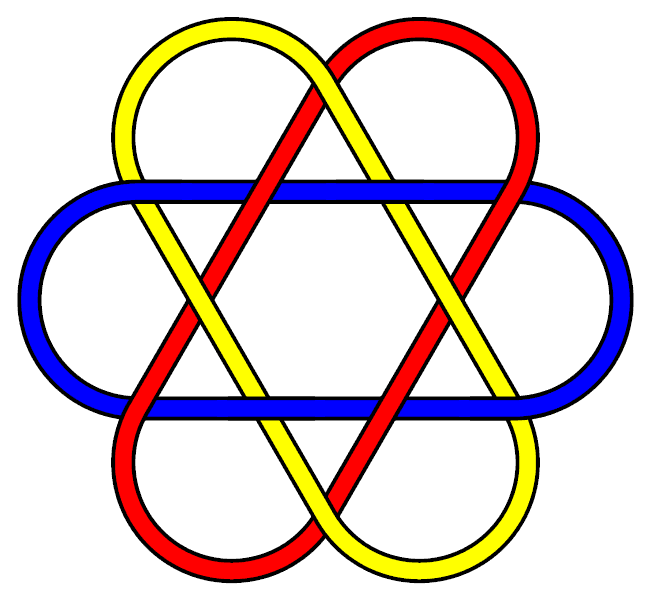
The best-known and simplest possible Brunnian link is the Borromean rings, a link of three unknots. (This is also the only Brunnian link with less than 10 crossings, and the only symmetrical Brunnian link with less than 12 crossings.) However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings:
12-crossing link.
18-crossing link.
24-crossing link.
30-crossing link.
T. Kanenobu has proven there exist hyperbolic Brunnian links with arbitrarily many components.
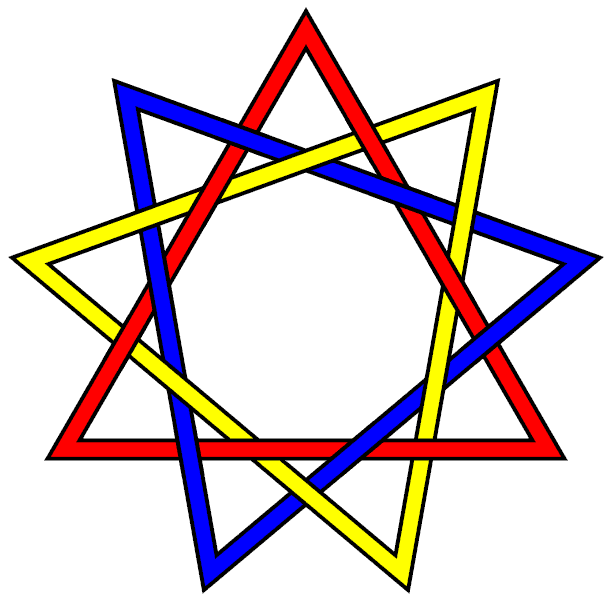
Non-Borromean-rings Brunnian links in real world symbols
A version of the three interlaced triangles (18-crossings Brunnian link) is also found in the sixth century Marundheeswarar Temple in Thiruvanmayur, South Chennai, India, associated with the goddess Tripurasundari,[1] and is occasionally called "the star of the muses" as a minor symbol in some New Age / occultist / neo-pagan circles.
See also
Further reading
T.Kanenobu, Hyperbolic links with Brunnian properties. J. Math. Soc. Japan. Vol 38 No. 2, (1986) 295--308.
