Naming and Enumeration: Difference between revisions
(temporarily reverting scott's changes) |
(restoring scott's changes, except for the quotes.) |
||
| Line 73: | Line 73: | ||
<!--END--> |
<!--END--> |
||
Thus at the moment there are |
Thus at the moment there are 1701936 knots and 5700 links known to <code>KnotTheory`</code>: |
||
<!--$$Length /@ {AllKnots[], AllLinks[]}$$--> |
<!--$$Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = 9 | |
n = 9 | |
||
in = <nowiki>Length /@ {AllKnots[], AllLinks[]}</nowiki> | |
in = <nowiki>Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}</nowiki> | |
||
out= <nowiki>{802, 1424}</nowiki>}} |
out= <nowiki>{802, 1424}</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 105: | Line 105: | ||
out= <nowiki>TorusKnot[m, n] represents the (m,n) torus knot.</nowiki>}} |
out= <nowiki>TorusKnot[m, n] represents the (m,n) torus knot.</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
<!--$$?TorusKnots$$--> |
|||
For example, the torus knots [[T(5,3)]] and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant <math>V_3</math>): |
For example, the torus knots [[T(5,3)]] and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant <math>V_3</math>): |
||
| Line 125: | Line 126: | ||
KnotTheory` knows how to plot torus knots; see [[Drawing with TubePlot]]. |
KnotTheory` knows how to plot torus knots; see [[Drawing with TubePlot]]. |
||
You can also use the function Knot to parse certain string representations of named knots: |
|||
In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas. |
|||
<!--$$NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}$$--> |
|||
== References== |
== References== |
||
Revision as of 15:59, 14 February 2006
KnotTheory` comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings [Rolfsen], the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see Knotscape):
(For In[1] see Setup)
| ||||
| ||||
 6_1 |
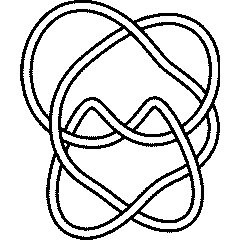 9_46 |
Thus, for example, let us verify that the knots 6_1 and 9_46 have the same Alexander polynomial:
In[4]:=
|
Alexander[Knot[6, 1]][t]
|
Out[4]=
|
2
5 - - - 2 t
t
|
In[5]:=
|
Alexander[Knot[9, 46]][t]
|
Out[5]=
|
2
5 - - - 2 t
t
|
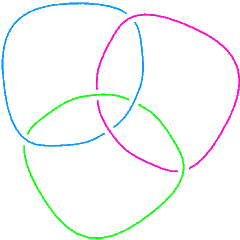 L6a4 |
We can also check that the Borromean rings, L6a4 in the Thistlethwaite table, is a 3-component link:
In[6]:=
|
Length[Skeleton[Link[6, Alternating, 4]]]
|
Out[6]=
|
3
|
| ||||
| ||||
Thus at the moment there are 1701936 knots and 5700 links known to KnotTheory`:
In[9]:=
|
Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}
|
Out[9]=
|
{802, 1424}
|
In[10]:=
|
Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]
|
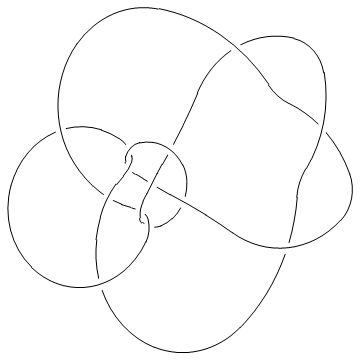
| |
Out[10]=
|
-Graphics-
|
(Shumakovitch had noticed that this nice knot has interesting Khovanov homology; see [Shumakovitch]).
 T(5,3) |
In addition to the tables, KnotTheory` also knows about torus knots:
| ||||
For example, the torus knots T(5,3) and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant ):
In[12]:=
|
Crossings /@ {TorusKnot[5,3], TorusKnot[3, 5]}
|
Out[12]=
|
{10, 12}
|
In[13]:=
|
Vassiliev[3] /@ {TorusKnot[5,3], TorusKnot[3, 5]}
|
Out[13]=
|
{20, 20}
|
KnotTheory` knows how to plot torus knots; see Drawing with TubePlot.
You can also use the function Knot to parse certain string representations of named knots:
In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas.
References
[Rolfsen] ^ D. Rolfsen, Knots and Links, Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976.
[Shumakovitch] ^ A. Shumakovitch, Torsion of the Khovanov Homology, arXiv:math.GT/0405474.
