DT (Dowker-Thistlethwaite) Codes: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
====Knots==== |
|||
The "DT Code" ("DT" after [http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Dowker.html Clifford Hugh Dowker] and [http://www.math.utk.edu/~morwen/ Morwen Thistlethwaite]) of a knot <math>K</math> is obtained as follows: |
The "DT Code" ("DT" after [http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Dowker.html Clifford Hugh Dowker] and [http://www.math.utk.edu/~morwen/ Morwen Thistlethwaite]) of a knot <math>K</math> is obtained as follows: |
||
* Start "walking" along <math>K</math> and count every crossing you pass through. If <math>K</math> has <math>n</math> crossings and given that every crossing is visited twice, the count ends at <math>2n</math>. Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "under" the crossing. |
* Start "walking" along <math>K</math> and count every crossing you pass through. If <math>K</math> has <math>n</math> crossings and given that every crossing is visited twice, the count ends at <math>2n</math>. Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "under" the crossing. |
||
* Every crossing is now labeled with two integers whose absolute values run from <math>1</math> to <math>2n</math>. It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of <math>K</math> is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. |
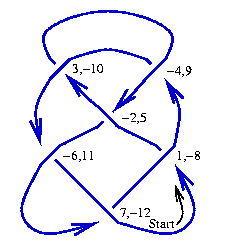
* Every crossing is now labeled with two integers whose absolute values run from <math>1</math> to <math>2n</math>. It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of <math>K</math> is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. Thus for example the pairing for the knot in the figure below is <math>((1,8), (3,10), (5,2), (7,12), (9,4), (11,6))</math>, and hence its DT code is <math>(8,10,2,12,4,6)</math>. |
||
[[Image:DTNotation.gif|frame|The <code>DT</code> notation|center]] |
[[Image:DTNotation.gif|frame|The <code>DT</code> notation|center]] |
||
| Line 69: | Line 70: | ||
out= <nowiki>PD[X[4, 2, 5, 1], X[6, 4, 1, 3], X[2, 6, 3, 5]]</nowiki>}} |
out= <nowiki>PD[X[4, 2, 5, 1], X[6, 4, 1, 3], X[2, 6, 3, 5]]</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
====Links==== |
|||
DT Codes for links are defined in a similar way (see {{ref|DollHoste}}). Follow the same numbering process as for knots, except when you finish traversing one component, jump straight to the next. It is not difficult to see that there is always a choice of starting points along the components for which the resulting pairing is a pairing between odd and even numbers. Again, it is enough to only list the even numbers corresponding to <math>1, 3, 5, \ldots</math>. |
|||
{{note|DollHoste}} H. Doll and J. Hoste, ''A tabulation of oriented links'', Mathematics of Computation '''57-196''' (1991) 747-761. |
|||
Revision as of 17:26, 14 February 2006
Knots
The "DT Code" ("DT" after Clifford Hugh Dowker and Morwen Thistlethwaite) of a knot is obtained as follows:
- Start "walking" along and count every crossing you pass through. If has crossings and given that every crossing is visited twice, the count ends at . Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "under" the crossing.
- Every crossing is now labeled with two integers whose absolute values run from to . It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. Thus for example the pairing for the knot in the figure below is , and hence its DT code is .
KnotTheory` has some rudimentary support for DT codes:
(For In[1] see Setup)
| ||||
Thus for example, the DT codes for the last 9 crossing alternating knot 9_41 and the first 9 crossing non alternating knot 9_42 are:
In[2]:=
|
dts = DTCode /@ {Knot[9, 41], Knot[9, 42]}
|
Out[2]=
|
{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8],
DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}
|
(The DT code of an alternating knot is always a sequence of positive numbers but the DT code of a non alternating knot contains both signs.)
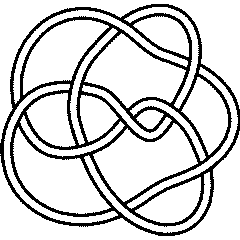 9_41 |
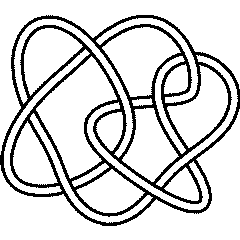 9_42 |
DT codes and Gauss codes carry the same information and are easily convertible:
In[3]:=
|
gcs = GaussCode /@ dts
|
Out[3]=
|
{GaussCode[1, -6, 2, -8, 3, -1, 4, -9, 5, -2, 6, -4, 7, -3, 8, -5, 9,
-7], GaussCode[1, -5, 2, -1, 3, 8, -4, -2, 5, -3, -6, 9, -7, 4, -8,
6, -9, 7]}
|
In[4]:=
|
DTCode /@ gcs
|
Out[4]=
|
{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8],
DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}
|
Conversion between DT codes and/or Gauss codes and PD codes is more complicated; the harder side, going from DT/Gauss to PD, was written by Siddarth Sankaran at the University of Toronto:
In[5]:=
|
PD[DTCode[4, 6, 2]]
|
Out[5]=
|
PD[X[4, 2, 5, 1], X[6, 4, 1, 3], X[2, 6, 3, 5]]
|
Links
DT Codes for links are defined in a similar way (see [DollHoste]). Follow the same numbering process as for knots, except when you finish traversing one component, jump straight to the next. It is not difficult to see that there is always a choice of starting points along the components for which the resulting pairing is a pairing between odd and even numbers. Again, it is enough to only list the even numbers corresponding to .
[DollHoste] ^ H. Doll and J. Hoste, A tabulation of oriented links, Mathematics of Computation 57-196 (1991) 747-761.