Braid Representatives

chiracrelc4

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:

(For In[1] see Setup)

In[1]:= ?BR BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot.

In[2]:= BR::about The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See his article on the subject at arXiv:math.GT/0401051. Vogel's algorithm was implemented by Dan Carney in the summer of 2005 at the University of Toronto.

In[3]:= ?Mirror Mirror[br] return the mirror braid of br.

Thus for example,

In[4]:=

br1 = BR[2, {-1, -1, -1}];

In[5]:=	PD[br1]
Out[5]=	PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]

In[6]:=	Jones[br1][q]
Out[6]=	-4 -3 1 -q + q + - q

In[7]:=	Mirror[br1]
Out[7]=	BR[2, {1, 1, 1}]

T(5,4)

K11a362

KnotTheory` has the braid representatives of some knots and links pre-loaded, and for all other knots and links it will find a braid representative using Vogel's algorithm. Thus for example,

In[8]:=	BR[TorusKnot[5, 4]]
Out[8]=	BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]

In[9]:=	BR[Knot[11, Alternating, 362]]
Out[9]=	BR[10, {1, 2, -3, -4, 5, 6, 5, 4, 3, -2, -1, -4, 3, -2, -4, 3, 5, 4, -6, 7, -6, 5, 8, 7, 6, 5, -4, -3, 2, 5, -6, 9, -8, 7, -6, 5, 4, -3, 5, 6, 5, 4, 5, -7, 8, -7, 6, 5, -9, -8, -7}]

(As we see, Vogel's algorithm sometimes produces scary results. A 51-crossings braid representative for an 11-crossing knot, in the case of K11a362).

10_1

5_2

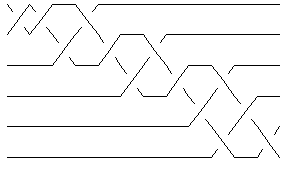
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot 10_1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):

In[10]:=	br2 = BR[Knot[10, 1]]
Out[10]=	BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]

In[12]:=	Show[BraidPlot[CollapseBraid[br2]]]
Out[12]=	-Graphics-

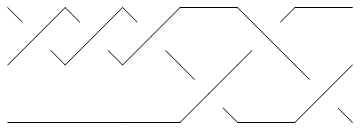
Already for the knot 5_2 the minimum braid is shorter than the braid produced by Vogel's algorithm. Indeed, the minimum braid is

In[14]:=	Show[BraidPlot[CollapseBraid[BR[Knot[5, 2]]]]]
Out[14]=	-Graphics-

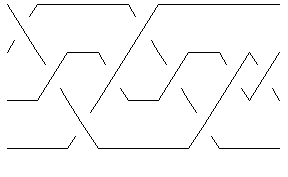
To force KnotTheory` to run Vogel's algorithm on 5_2, we first convert it to its PD form,

In[15]:=	pd = PD[Knot[5, 2]]
Out[15]=	PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 10, 6, 1], X[9, 6, 10, 7], X[7, 2, 8, 3]]

and only then run BR:

In[17]:=	Show[BraidPlot[CollapseBraid[BR[pd]]]]
Out[17]=	-Graphics-

(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)

[Gittings] ^  T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.