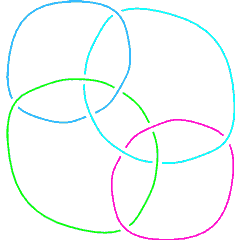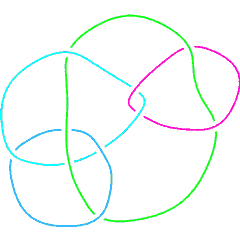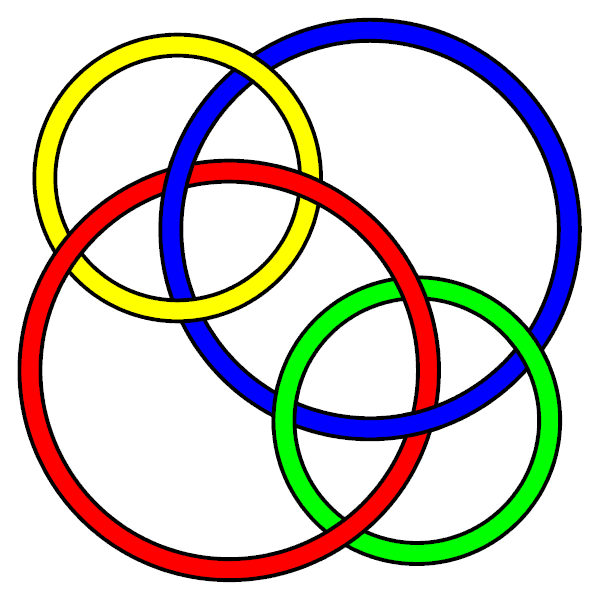L10n107
From Knot Atlas
Jump to navigationJump to search
|
|
|
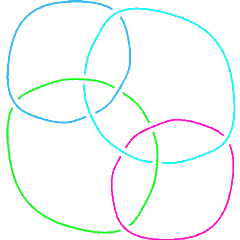 (Knotscape image) |
See the full Thistlethwaite Link Table (up to 11 crossings). |
|
L10n107 is the "Borromean chain mail" link - it contains two L6a4 configurations without any L2a1 configuration (i.e. no two loops are linked). Compare L10a169. |
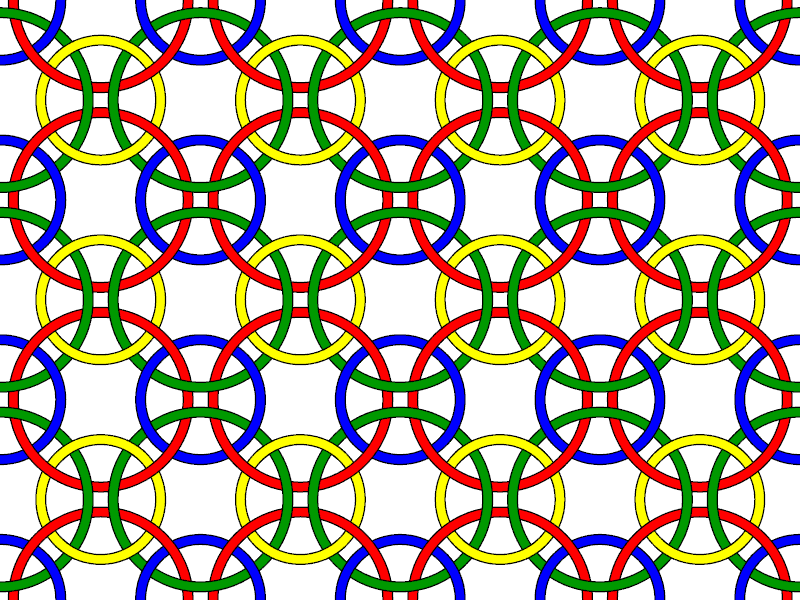
An indefinitely extended "Borromean chainmail" pattern made up of overlapping L10n107 links; no two circles are directly linked.
Link Presentations
[edit Notes on L10n107's Link Presentations]
| Planar diagram presentation | X6172 X5,12,6,13 X8493 X2,16,3,15 X16,7,17,8 X9,11,10,14 X13,15,14,20 X19,5,20,10 X11,18,12,19 X4,17,1,18 |
| Gauss code | {1, -4, 3, -10}, {-9, 2, -7, 6}, {-2, -1, 5, -3, -6, 8}, {4, -5, 10, 9, -8, 7} |
| A Braid Representative | {{{braid_table}}} |
| A Morse Link Presentation | 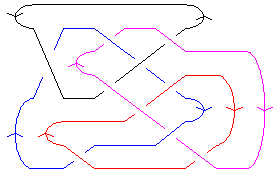
|
Polynomial invariants
| Multivariable Alexander Polynomial (in , , , ...) | (db) |
| Jones polynomial | (db) |
| Signature | 0 (db) |
| HOMFLY-PT polynomial | (db) |
| Kauffman polynomial | (db) |
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). |
|
| Integral Khovanov Homology
(db, data source) |
|
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
Modifying This Page
| Read me first: Modifying Knot Pages
See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top. |
|