DT (Dowker-Thistlethwaite) Codes

KnotTheory`/Navigation

The Mathematica Package KnotTheory`

Knots

The "DT Code" ("DT" after Clifford Hugh Dowker and Morwen Thistlethwaite) of a knot $K$ is obtained as follows:

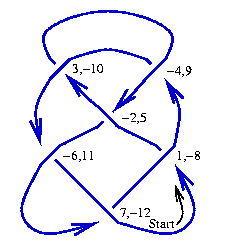
Start "walking" along $K$ and count every crossing you pass through. If $K$ has $n$ crossings and given that every crossing is visited twice, the count ends at $2n$ . Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "over" the crossing.
Every crossing is now labeled with two integers whose absolute values run from $1$ to $2n$ . It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of $K$ is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. Thus for example the pairing for the knot in the figure below is $((1,-8),(3,-10),(5,-2),(7,-12),(9,-4),(11,-6))$ , and hence its DT code is $(-8,-10,-2,-12,-4,-6)$ (and as DT codes are insensitive to overall mirrors, this is equivalent to $(8,10,2,12,4,6)$ ).

The DT notation

KnotTheory` has some rudimentary support for DT codes:

(For In[1] see Setup)

In[2]:=	?DTCode
DTCode[i1, i2, ...] represents a knot via its DT (Dowker-Thistlethwaite) code, while DTCode[{i11,...}, {i21...}, ...] likewise represents a link. DTCode also acts as a "type caster", so for example, DTCode[K] where K is is a named knot or link returns the DT code of K.

Thus for example, the DT codes for the last 9 crossing alternating knot 9_41 and the first 9 crossing non alternating knot 9_42 are:

`In[3]:=`	`dts = DTCode /@ {Knot[9, 41], Knot[9, 42]}`
`Out[3]=`	`{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8], DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}`

(The DT code of an alternating knot is always a sequence of positive numbers but the DT code of a non alternating knot contains both signs.)

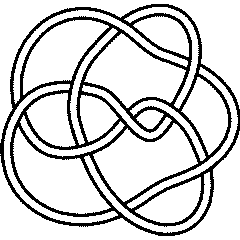9_41

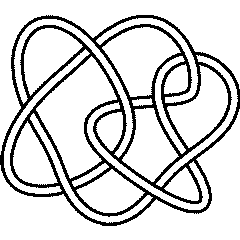9_42

DT codes and Gauss codes carry the same information and are easily convertible:

`In[4]:=`	`gcs = GaussCode /@ dts`
`Out[4]=`	`{GaussCode[1, -6, 2, -8, 3, -1, 4, -9, 5, -2, 6, -4, 7, -3, 8, -5, 9, -7], GaussCode[1, -5, 2, -1, 3, 8, -4, -2, 5, -3, -6, 9, -7, 4, -8, 6, -9, 7]}`

`In[5]:=`	`DTCode /@ gcs`
`Out[5]=`	`{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8], DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}`

Conversion between DT codes and/or Gauss codes and PD codes is more complicated; the harder side, going from DT/Gauss to PD, was written by Siddarth Sankaran at the University of Toronto:

`In[6]:=`	`PD[DTCode[4, 6, 2]]`
`Out[6]=`	`PD[X[4, 2, 5, 1], X[6, 4, 1, 3], X[2, 6, 3, 5]]`

Links

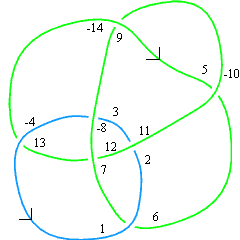
A DT notation example, for the link L7n2

DT Codes for links are defined in a similar way (see [DollHoste]). Follow the same numbering process as for knots, except when you finish traversing one component, jump straight to the next. It is not difficult to see that there is always a choice of starting points along the components for which the resulting pairing is a pairing between odd and even numbers. (On the figure above one possible choice is indicated). Again, it is enough to only list the even numbers corresponding to $1,3,5,\ldots$ ; call the resulting list $\lambda$ . (Above, $\lambda =(6,-8,-10,12,-14,2,-4)$ ). Notice that the odd indices are naturally subdivided into sublists according to the component of the link on which they lie, and this induces a subdivision of $\lambda$ into sublists. Thus with the choices made in the figure above, the DT code for the link L7n2 is $(6,-8\mid -10,12,-14,2,-4)$ .

KnotTheory` knows about DT codes for links:

`In[7]:=`	`DTCode[Link[7, NonAlternating, 2]]`
`Out[7]=`	`DTCode[{6, -8}, {-10, 12, -14, 2, -4}]`

`In[8]:=`	`MultivariableAlexander[DTCode[{6, -8}, {-10, 12, -14, 2, -4}]][t]`
`Out[8]=`	`-1 + t[1] + t[2] - t[1] t[2]`

[DollHoste] ^ H. Doll and J. Hoste, A tabulation of oriented links, Mathematics of Computation 57-196 (1991) 747-761.

DT (Dowker-Thistlethwaite) Codes

Knots

Links

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

Tools