The Multivariable Alexander Polynomial: Difference between revisions
No edit summary |
m (Reverted edit of 218.237.225.29, changed back to last version by Drorbn) |
||
| Line 26: | Line 26: | ||
t[1] -> t1, t[2] -> t2, t[3] -> t4, t[4] -> t3 |
t[1] -> t1, t[2] -> t2, t[3] -> t4, t[4] -> t3 |
||
}</nowiki> | |
}</nowiki> | |
||
out= <nowiki>-t1 - t2 |
out= <nowiki>-t1 - t2 + t1 t2 - t3 + 2 t1 t3 + t2 t3 - t1 t2 t3 - t4 + t1 t4 + |
||
2 t2 t4 - t1 t2 t4 |
2 t2 t4 - t1 t2 t4 + t3 t4 - t1 t3 t4 - t2 t3 t4</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 44: | Line 44: | ||
n = 6 | |
n = 6 | |
||
in = <nowiki>mva - (mva /. {t1->t2, t2->t1})</nowiki> | |
in = <nowiki>mva - (mva /. {t1->t2, t2->t1})</nowiki> | |
||
out= <nowiki>t1 t3 - t2 t3 - t1 t4 |
out= <nowiki>t1 t3 - t2 t3 - t1 t4 + t2 t4</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 53: | Line 53: | ||
There are 11 links with up to 11 crossings whose multivariable Alexander polynomial is <math>0</math>. Here they are: |
There are 11 links with up to 11 crossings whose multivariable Alexander polynomial is <math>0</math>. Here they are: |
||
<!--$$Select[AllLinks[], (MultivariableAlexander[#][t] == 0) |
<!--$$Select[AllLinks[], (MultivariableAlexander[#][t] == 0) &]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 7 | |
|||
in = <nowiki>Select[AllLinks[], (MultivariableAlexander[#][t] == 0) &]</nowiki> | |
|||
out= <nowiki>{Link[9, NonAlternating, 27], Link[10, NonAlternating, 32], |
|||
Link[10, NonAlternating, 36], Link[10, NonAlternating, 107], |
|||
Link[11, NonAlternating, 244], Link[11, NonAlternating, 247], |
|||
Link[11, NonAlternating, 334], Link[11, NonAlternating, 381], |
|||
Link[11, NonAlternating, 396], Link[11, NonAlternating, 404], |
|||
Link[11, NonAlternating, 406]}</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Quadruple|L9n27|gif|L10n32|gif|L10n36|gif|L10n107|gif}} |
|||
{{Knot Image Quadruple|L11n244|gif|L11n247|gif|L11n334|gif|L11n381|gif}} |
|||
{{Knot Image Triple|L11n396|gif|L11n404|gif|L11n406|gif}} |
|||
[[User:Drorbn|Dror]] doesn't understand the multivariable Alexander polynomial well enough to give simple topological reasons for the vanishing of the said polynomial for these knots. |
|||
Revision as of 07:39, 13 April 2007
(For In[1] see Setup)
|
| ||||||||
 L8a21 |
The link L8a21 is symmetric under cyclic permutations of its components but not under interchanging two adjacent components. It is amusing to see how this is reflected in its multivariable Alexander polynomial:
In[4]:=
|
mva = MultivariableAlexander[Link[8, Alternating, 21]][t] /. {
t[1] -> t1, t[2] -> t2, t[3] -> t4, t[4] -> t3
}
|
Out[4]=
|
-t1 - t2 + t1 t2 - t3 + 2 t1 t3 + t2 t3 - t1 t2 t3 - t4 + t1 t4 +
2 t2 t4 - t1 t2 t4 + t3 t4 - t1 t3 t4 - t2 t3 t4
|
In[5]:=
|
mva - (mva /. {t1->t2, t2->t3, t3->t4, t4->t1})
|
Out[5]=
|
0
|
In[6]:=
|
mva - (mva /. {t1->t2, t2->t1})
|
Out[6]=
|
t1 t3 - t2 t3 - t1 t4 + t2 t4
|
But notice the funny labelling of the components! At the moment there is no way to tell MultivariableAlexander which variable is to be associated with what variable so MultivariableAlexander chooses an arbitrary ordering of tha variables. Hence we had to rename t[3] to be t4 and t[4] to be t3.
(To be precise, MultivariableAlexander orders the components so that its output would be lexicographically minimal among all possible orderings. This way it is at least guaranteed that different presentations for the same link will yield the same output for MultivariableAlexander.)
There are 11 links with up to 11 crossings whose multivariable Alexander polynomial is . Here they are:
In[7]:=
|
Select[AllLinks[], (MultivariableAlexander[#][t] == 0) &]
|
Out[7]=
|
{Link[9, NonAlternating, 27], Link[10, NonAlternating, 32],
Link[10, NonAlternating, 36], Link[10, NonAlternating, 107],
Link[11, NonAlternating, 244], Link[11, NonAlternating, 247],
Link[11, NonAlternating, 334], Link[11, NonAlternating, 381],
Link[11, NonAlternating, 396], Link[11, NonAlternating, 404],
Link[11, NonAlternating, 406]}
|
 L9n27 |
 L10n32 |
 L10n36 |
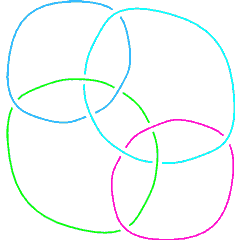 L10n107 |
 L11n244 |
 L11n247 |
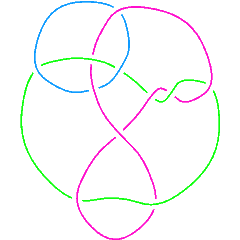 L11n334 |
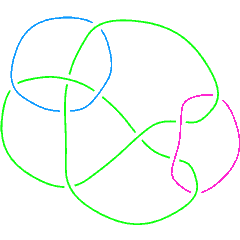 L11n381 |
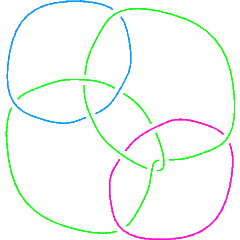 L11n396 |
 L11n404 |
 L11n406 |
Dror doesn't understand the multivariable Alexander polynomial well enough to give simple topological reasons for the vanishing of the said polynomial for these knots.
