The Determinant and the Signature: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (23 intermediate revisions by 4 users not shown) | |||
| Line 3: | Line 3: | ||
{{Startup Note}} |
{{Startup Note}} |
||
<!--$$?KnotDet$$--> |
<!--$$?KnotDet$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 2 | |
|||
in = <nowiki>KnotDet</nowiki> | |
|||
out= <nowiki>KnotDet[K] returns the determinant of a knot K.</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$?KnotSignature$$--> |
<!--$$?KnotSignature$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 3 | |
|||
in = <nowiki>KnotSignature</nowiki> | |
|||
out= <nowiki>KnotSignature[K] returns the signature of a knot K.</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
Thus, for example, the knots [[5_1]] and [[10_132]] have the same determinant (and even the same Alexander and Jones polynomials), but different signatures: |
Thus, for example, the knots [[5_1]] and [[10_132]] have the same determinant (and even the same Alexander and Jones polynomials), but different signatures: |
||
{{Knot Image Pair|5_1|gif|10_132|gif}} |
|||
<center>[[Image:5_1.gif|frame|none|<center>[[5_1]]</center>]] [[Image:10_132.gif|frame|none|<center>[[10_132]]</center>]]</center> |
|||
<!--$$KnotDet /@ {Knot[5, 1], Knot[10, 132]}$$--> |
<!--$$KnotDet /@ {Knot[5, 1], Knot[10, 132]}$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 4 | |
|||
in = <nowiki>KnotDet /@ {Knot[5, 1], Knot[10, 132]}</nowiki> | |
|||
out= <nowiki>{5, 5}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
<!--$${ |
|||
| ⚫ | |||
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}), |
|||
| ⚫ | |||
}$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 5 | |
|||
in = <nowiki>{ |
|||
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}), |
|||
Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]}) |
|||
}</nowiki> | |
|||
out= <nowiki>{True, True}</nowiki>}} |
|||
<!--END--> |
|||
<!--$$KnotSignature /@ {Knot[5, 1], Knot[10, 132]}$$--> |
<!--$$KnotSignature /@ {Knot[5, 1], Knot[10, 132]}$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 6 | |
|||
in = <nowiki>KnotSignature /@ {Knot[5, 1], Knot[10, 132]}</nowiki> | |
|||
out= <nowiki>{-4, 0}</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
In August 2005 somebody emailed [[User:Drorbn|Dror]] a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is <math>\pm 1</math>". So on September 2<sup>nd</sup> Dror typed |
|||
<!--$$Select[AllKnots[], Abs[KnotDet[#]] == 1 &]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 7 | |
|||
in = <nowiki>Select[AllKnots[], Abs[KnotDet[#]] == 1 &]</nowiki> | |
|||
out= <nowiki>{Knot[0, 1], Knot[10, 124], Knot[10, 153], |
|||
Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42], |
|||
Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}</nowiki>}} |
|||
<!--END--> |
|||
Hence the first few knots that are not <math>k</math>-colourable for any <math>k</math> are [[10_124]], [[10_153]], [[K11n34]], [[K11n42]], [[K11n49]] and [[K11n116]]. |
|||
{{Knot Image|K11n116|gif}} |
|||
Latest revision as of 17:21, 21 February 2013
(For In[1] see Setup)
| ||||
| ||||
Thus, for example, the knots 5_1 and 10_132 have the same determinant (and even the same Alexander and Jones polynomials), but different signatures:
 5_1 |
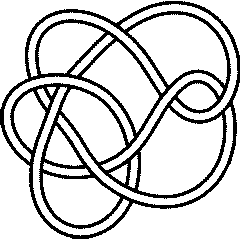 10_132 |
In[4]:=
|
KnotDet /@ {Knot[5, 1], Knot[10, 132]}
|
Out[4]=
|
{5, 5}
|
In[5]:=
|
{
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}),
Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]})
}
|
Out[5]=
|
{True, True}
|
In[6]:=
|
KnotSignature /@ {Knot[5, 1], Knot[10, 132]}
|
Out[6]=
|
{-4, 0}
|
In August 2005 somebody emailed Dror a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is ". So on September 2nd Dror typed
In[7]:=
|
Select[AllKnots[], Abs[KnotDet[#]] == 1 &]
|
Out[7]=
|
{Knot[0, 1], Knot[10, 124], Knot[10, 153],
Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42],
Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}
|
Hence the first few knots that are not -colourable for any are 10_124, 10_153, K11n34, K11n42, K11n49 and K11n116.
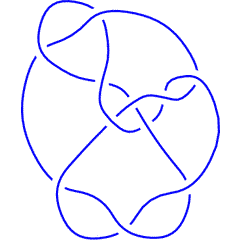 K11n116 |

