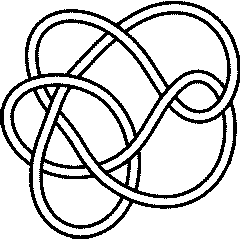The Determinant and the Signature: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 69: | Line 69: | ||
<!--END--> |
<!--END--> |
||
Hence the first few knots that are not <math>k</math>-colourable for any <math>k</math> are [[10_124]], [[10_153]], [[K11n34]], [[K11n42]], [[K11n49]] and [[K11n116]]. |
|||
{{Knot Image|K11n116|gif}} |
{{Knot Image|K11n116|gif}} |
||
Revision as of 09:27, 2 September 2005
(For In[1] see Setup)
| ||||
| ||||
Thus, for example, the knots 5_1 and 10_132 have the same determinant (and even the same Alexander and Jones polynomials), but different signatures:
In[3]:=
|
KnotDet /@ {Knot[5, 1], Knot[10, 132]}
|
Out[3]=
|
{5, 5}
|
In[4]:=
|
{
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}),
Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]})
}
|
Out[4]=
|
{True, True}
|
In[5]:=
|
KnotSignature /@ {Knot[5, 1], Knot[10, 132]}
|
Out[5]=
|
{-4, 0}
|
In August 2005 somebody emailed Dror a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is . So on September 2nd Dror typed
In[6]:=
|
Select[AllKnots[], Abs[KnotDet[#]] == 1 &]
|
Out[6]=
|
{Knot[0, 1], Knot[10, 124], Knot[10, 153],
Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42],
Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}
|
Hence the first few knots that are not -colourable for any are 10_124, 10_153, K11n34, K11n42, K11n49 and K11n116.
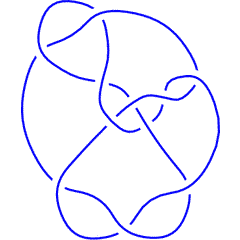 K11n116 |